
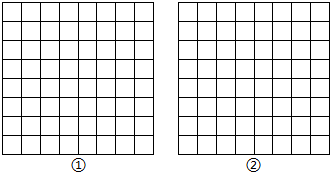
 如图,正方形网格中的每一个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别在图①、图②中,画三角形和平行四边形.
如图,正方形网格中的每一个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别在图①、图②中,画三角形和平行四边形.科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 48+20$\sqrt{3}$ | B. | 32+20$\sqrt{3}$ | C. | 52+16$\sqrt{3}$ | D. | 28+16$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
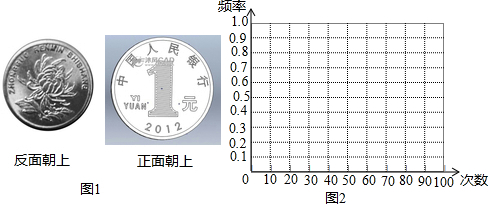
| 实验次数n | 10 | 20 | 30 | 40 | 50 | 60 | 80 | 100 |
| 正面朝上的次数m | 7 | 12 | 15 | 18 | 27 | 27 | 44 | 49 |
| 正面朝上的频率$\frac{m}{n}$ | 0.7 | 0.6 | 0.5 | 0.45 | 0.54 | 0.45 | 0.55 | 0.49 |
| 反面朝上的次数p | 3 | 8 | 15 | 22 | 23 | 33 | 36 | 51 |
| 反面朝上的频率$\frac{p}{n}$ | 0.3 | 0.4 | 0.5 | 0.55 | 0.46 | 0.55 | 0.45 | 0.51 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是一个正方形盒子的展开图,若要在展开后的其中的三个正方形A、B、C内分别填入适当的数,使得展开图折成正方体后相对的面上的两个数互为相反数,则填入正方形A、B、C内的三个数依次为( )
如图,是一个正方形盒子的展开图,若要在展开后的其中的三个正方形A、B、C内分别填入适当的数,使得展开图折成正方体后相对的面上的两个数互为相反数,则填入正方形A、B、C内的三个数依次为( )| A. | 1,-2,0 | B. | 0,-2,1 | C. | -2,0,1 | D. | -2,1,0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6 | B. | -4 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A,B两地之间有一座山,汽车原来从A地到B地需经C地沿折线A-C-B行驶,现开通隧道后,汽车直接沿直线AB行驶即可到达B地.已知AC=120千米,∠A=30°,∠B=135°,求隧道开通后汽车从A地到B地行驶多少千米?
如图,A,B两地之间有一座山,汽车原来从A地到B地需经C地沿折线A-C-B行驶,现开通隧道后,汽车直接沿直线AB行驶即可到达B地.已知AC=120千米,∠A=30°,∠B=135°,求隧道开通后汽车从A地到B地行驶多少千米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com