Question

△ABC是一块等边三角形的废铁片，利用其剪裁一个正方形DEFG，使正方形的一条边DE落在BC上，顶点F、G分别落在AC、AB上．

   Ⅰ．证明：△BDG≌△CEF；

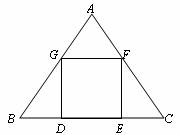
Ⅱ．探究：怎样在铁片上准确地画出正方形．

小聪和小明各给出了一种想法，请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答．

Ⅱa．小聪想：要画出正方形DEFG，只要能计算出正方形的边长就能求出BD和CE的长，从而确定D点和E点，再画正方形DEFG就容易了．

设△ABC的边长为2 ，请你帮小聪求出正方形的边长(结果用含根号的式子表示，不要求分母有理化) ．

Ⅱb．小明想：不求正方形的边长也能画出正方形． 具体作法是：

      ①在AB边上任取一点G’，如图作正方形G’D’E’F’；

②连结BF’并延长交AC于F；

③作FE∥F’E’交BC于E，FG∥F′G′交AB于G，GD∥G’D’交BC于D，则四边形DEFG即为所求．

你认为小明的作法正确吗？说明理由．

Answer 1

Ⅰ．证明：∵DEFG为正方形，

∴GD=FE，∠GDB=∠FEC=90°

      ∵△ABC是等边三角形，∴∠B=∠C=60°

      ∴△BDG≌△CEF(AAS)

    Ⅱa．解法一：

设正方形的边长为x，作△ABC的高AH，

求得

由△AGF∽△ABC得：

解之得：(或)

解法二：设正方形的边长为x，则

　　　　在Rt△BDG中，tan∠B=，

∴

解之得：(或)

解法三：设正方形的边长为x，

则

由勾股定理得：

解之得：

Ⅱb．解：

 正确

由已知可知，四边形GDEF为矩形

∵FE∥F’E’ ，

∴，

同理，

∴

又∵F’E’=F’G’，

∴FE=FG

因此，矩形GDEF为正方形