
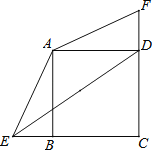
【题目】在正方形ABCD中,BC=2,E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF.
(1)求证:△ADF≌△ABE.
(2)若BE=1,求sin∠AED的值.
【答案】(1)见解析; (2) ![]()
【解析】
(1)根据正方形的性质可得AB=DA,∠ABE=∠ADF=90°,再根据DF=BE,即可证明△ADF≌△ABE(SAS).
(2)作AH⊥DE于H,由勾股定理得DE=![]() ,AE=
,AE=![]() ,根据三角形面积公式求出AH=
,根据三角形面积公式求出AH=![]() ,即可求出sin∠AED的值.
,即可求出sin∠AED的值.
解:(1)∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,
∴∠ABE=∠ADF=90°,
在△ADF和△ABE中:
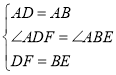
∴△ADF≌△ABE(SAS).
(2)∵BC=2,BE=1,
∴CD=AD=AB=2,CE=3,
∴DE=![]() =
=![]() ,AE=
,AE=![]() =
=![]() ,
,
如图,作AH⊥DE于H,
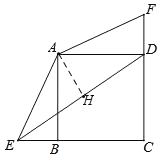
则S△AED=![]() DEAH,
DEAH,
又∵S△AED=![]() ADAB=2,
ADAB=2,
∴![]() DEAH=2,
DEAH=2,
∴AH=![]() ,
,
∴sin∠AED=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(![]() ,
,![]() ),AB=1,AD=2.
),AB=1,AD=2.

(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数![]() (
(![]() )的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
)的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(4,0),C(0,2)三点.
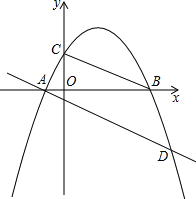
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E,使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
(3)若将直线BC平移,使其经过点A,且与抛物线相交于点D,连接BD,试求出∠BDA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,∠AOB=90°,AO=3BO,OB在x轴上,将Rt△AOB绕点O顺时针旋转至△RtA'OB',其中点B'落在反比例函数y=﹣![]() 的图象上,OA'交反比例函数y=
的图象上,OA'交反比例函数y=![]() 的图象于点C,且OC=2CA',则k的值为( )
的图象于点C,且OC=2CA',则k的值为( )

A. 4 B. ![]() C. 8 D. 7
C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师从学校出发,到距学校![]() 的某商场去给学生买奖品,他先步行了
的某商场去给学生买奖品,他先步行了![]() 后,换骑上了共享单车,到达商场时,全程总共刚好花了
后,换骑上了共享单车,到达商场时,全程总共刚好花了![]() .已知王老师骑共享单车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).
.已知王老师骑共享单车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).
(1)求王老师步行和骑共享单车的平均速度分别为多少?
(2)买完奖品后,王老师原路返回,为按时上班,路上所花时间最多只剩10分钟,若王老师仍采取先步行,后换骑共享单车的方式返回,问:他最多可步行多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com