
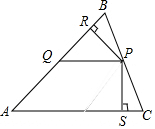
 如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR②AQ=PQ③△PQR≌△CPS,其中正确的是( )
如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR②AQ=PQ③△PQR≌△CPS,其中正确的是( )| A. | ①③ | B. | ①② | C. | ②③ | D. | ①②③ |
分析 连接AP,由已知条件利用角平行线的判定可得∠1=∠2,由三角形全等的判定得△APR≌△APS,得AS=AR,由已知可得∠2=∠3,得到∠1=∠3,得QP=AQ,答案可得.
解答 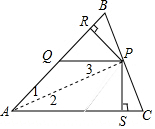 解:连接AP,∵PR=PS,PR⊥AB,垂足为R,PS⊥AC,垂足为S,
解:连接AP,∵PR=PS,PR⊥AB,垂足为R,PS⊥AC,垂足为S,
∴AP是∠BAC的平分线,∠1=∠2,
∴△APR≌△APS,
∴AS=AR,
又QP∥AR,
∴∠2=∠3,
又∠1=∠2,
∴∠1=∠3,
∴AQ=PQ,
没有办法证明△PQR≌△CPS,③不成立.
故选B.
点评 本题主要考查角平分线的判定和平行线的判定;准确作出辅助线是解决本题的关键,做题时要注意添加适当的辅助线,是十分重要的,要掌握.


科目:初中数学 来源: 题型:选择题
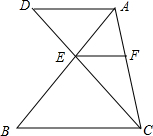 已知△ABC中,AD∥BC,CD交AB于E,EF∥BC,AE:EB=1:2,S△ADE=1,则S△AEF=( )
已知△ABC中,AD∥BC,CD交AB于E,EF∥BC,AE:EB=1:2,S△ADE=1,则S△AEF=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
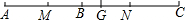 如图所示,G是线段AC的中点,点B在线段AC上,且M是线段AB的中点,N是线段BC的中点,那么下列等式成立的是( )
如图所示,G是线段AC的中点,点B在线段AC上,且M是线段AB的中点,N是线段BC的中点,那么下列等式成立的是( )| A. | MN=GC | B. | MG=$\frac{1}{2}$(AG-GB) | C. | GN=$\frac{1}{2}$(GC+GB) | D. | MN=$\frac{1}{2}$(AC+GB) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com