
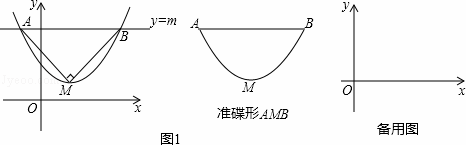
如图1,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的距离称为碟高.
(1)抛物线y=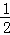 x2对应的碟宽
x2对应的碟宽 为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
(2)抛物线y=ax2﹣4ax﹣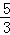 (a>0)对应的碟宽为6,且在x轴上,求a的值;
(a>0)对应的碟宽为6,且在x轴上,求a的值;
(3)将抛物线y=anx2+bnx+cn(an>0)的对应准蝶形记为Fn(n=1,2,3…),定义F1,F2,…,Fn为相似准蝶形,相应的碟宽之比即为相似比.若Fn与Fn﹣1的相似比为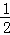 ,且Fn的碟顶是Fn﹣1的碟宽的中点,现将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
,且Fn的碟顶是Fn﹣1的碟宽的中点,现将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
①求抛物线y2的表达式;
②若F1的碟高为h1,F2的碟高为h2,…Fn的碟高为hn,则hn= ,Fn的碟宽有端点横坐标为 ;F1,F2,…,Fn的碟宽右端点是否在一条直线上?若是,直接写出该直线的表达式;若不是,请说明理由.
解:(1)4;1;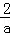 ;
;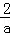 .
.
分析如下:
∵a>0,
∴y=ax2的图象大致如下:
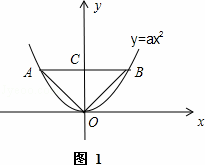
其必过原点O,记AB为其碟宽,AB与y轴的交点为C,连接OA,OB.
∵△DAB为等腰直角三角形,AB∥x轴,
∴OC⊥AB,
∴∠OCA=∠OCB=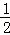 ∠AOB=
∠AOB=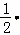 90°=45°,
90°=45°,
∴△ACO与△BCO亦为等腰直角三角形,
∴AC=OC=BC,
∴xA=yA,xB=yB,代入y=ax2,
∴A(﹣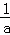 ,
,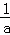 ),B(
),B(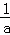 ,
,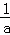 ),C(0,
),C(0,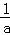 ),
),
∴AB=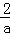 ,OC=
,OC=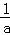 ,
,
即y=ax2的碟宽为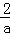 .
.
①抛物线y=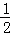 x2对应的a=
x2对应的a=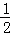 ,得碟宽
,得碟宽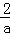 为4;
为4;
②抛物线y=4x2对应的a=4,得碟宽为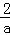 为
为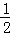 ;
;
③抛物线y=ax2(a>0),碟宽为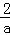 ;
;
④抛物线y=a(x﹣2)2+3(a>0)可看成y=ax2向右平移2个单位长度,再向上平移3个单位长度后得到的图形,
∵平移不改变形状、大小、方向,
∴抛物线y=a(x﹣2)2+3(a>0)的准碟形≌抛物线y=ax2的准碟,
∵抛物线y=ax2(a>0),碟宽为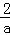 ,
,
∴抛物线y=a(x﹣2)2+3(a>0),碟宽为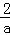 .
.
(2)∵y=ax2﹣4ax﹣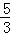 =a(x﹣2)2﹣(4a+
=a(x﹣2)2﹣(4a+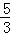 ),
),
∴同(1),其碟宽为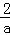 ,
,
∵y=ax2﹣4ax﹣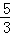 的碟宽为6,
的碟宽为6,
∴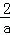 =6,
=6,
解得 a=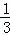 ,
,
∴y=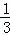 (x﹣2)2﹣3.
(x﹣2)2﹣3.
(3)①∵F1的碟宽:F2的碟宽=2:1,
∴ ,
,
∵a1=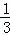 ,
,
∴a2=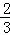 .
.
∵y=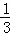 (x﹣2)2﹣3的碟宽AB在x轴上(A在B左边),
(x﹣2)2﹣3的碟宽AB在x轴上(A在B左边),
∴A(﹣1,0),B(5,0),
∴F2的碟顶坐标为(2,0),
∴y2=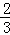 (x﹣2)2.
(x﹣2)2.
②∵Fn的准碟形为等腰直角三角形,
∴Fn的碟宽为2hn,
∵2hn:2hn﹣1=1:2,
∴hn=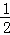 hn﹣1=(
hn﹣1=(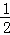 )2hn﹣2=(
)2hn﹣2=(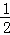 )3hn﹣3=…=(
)3hn﹣3=…=(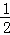 )n+1h1,
)n+1h1,
∵h1=3,
∴hn=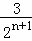 .
.
∵hn∥hn﹣1,且都过Fn﹣1的碟宽中点,
∴h1,h2,h3,…,hn﹣1,hn都在一条直线上,
∵h1在直线x=2上,
∴h1,h2,h3,…,hn﹣1,hn都在直线x=2上,
∴Fn的碟宽右端点横坐标为2+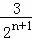 .
.
另,F1,F2,…,Fn的碟宽右端点在一条直线上,直线为y=﹣x+5.
分析如下:
考虑Fn﹣2,Fn﹣1,Fn情形,关系如图2,
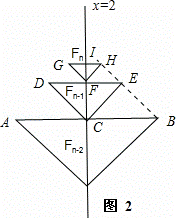
Fn﹣2,Fn﹣1,Fn的碟宽分别为AB,DE,GH;C,F,I分别为其碟宽的中点,都在直线x=2上,连接右端点,BE,EH.
∵AB∥x轴,DE∥x轴,GH∥x轴,
∴AB∥DE∥GH,
∴GH平行相等于FE,DE平行相等于CB,
∴四边形GFEH,四边形DCBE都为平行四边形,
∴HE∥GF,EB∥DC,
∵∠GFI= •∠GFH=
•∠GFH= •∠DCE=∠DCF,
•∠DCE=∠DCF,
∴GF∥DC,
∴HE∥EB,
∵HE,EB都过E点,
∴HE,EB在一条直线上,
∴Fn﹣2,Fn﹣1,Fn的碟宽的右端点是在一条直线,
∴F1,F2,…,Fn的碟宽的右端点是在一条直线.
∵F1:y1=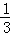 (x﹣2)2﹣3准碟形右端点坐标为(5,0),
(x﹣2)2﹣3准碟形右端点坐标为(5,0),
F2:y2=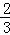 (x﹣2)2准碟形右端点坐标为(2+
(x﹣2)2准碟形右端点坐标为(2+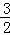 ,
,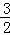 ),
),
∴待定系数可得过两点的直线为y=﹣x+5,
∴F1,F2,…,Fn的碟宽的右端点是在直线y=﹣x+5上.


科目:初中数学 来源: 题型:
2014年“五一”小长假,岳阳楼、君山岛景区接待游客约120000人次,将120000用科学记数法表示为( )
|
| A. | 12×104 | B. | 1.2×105 | C. | 1.2×106 | D. | 12万 |
查看答案和解析>>
科目:初中数学 来源: 题型:
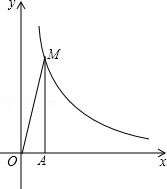
反比例函数y=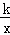 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数y=
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数y=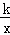 的图象于点M,△AOM的面积为3.
的图象于点M,△AOM的面积为3.
(1)求反比例函数的解析式;
(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数y=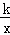 的图象上,求t的值.
的图象上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
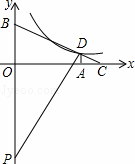
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=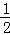 .延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3.
.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3.
(1)求点C的坐标;
(2)若点D在反比例函数y=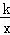 (k>0)的图象上,求反比例函数的解析式.
(k>0)的图象上,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列四个命题:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形;
(4)一组对边平行且相等的四边形是平行四边形.
其中正确的命题个数有( )
|
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
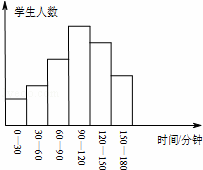
某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为 150 人.(注:横轴上每组数据包含最小值不包含最大值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com