
 如图,三条公路的交叉地带是一个三角形,经测量这个三角形的三条边长分别是AB=130米,BC=140米,AC=150米.市政府准备将其作为绿化用地,请你求出绿化用地的面积.
如图,三条公路的交叉地带是一个三角形,经测量这个三角形的三条边长分别是AB=130米,BC=140米,AC=150米.市政府准备将其作为绿化用地,请你求出绿化用地的面积.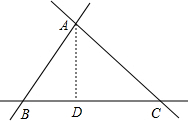 解:作BC边上的高AD,设BD=x米,则CD=(140-x)米,
解:作BC边上的高AD,设BD=x米,则CD=(140-x)米,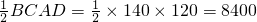 (米2)
(米2)

科目:初中数学 来源: 题型:
 如图,三条公路的交叉地带是一个三角形,经测量这个三角形的三条边长分别是AB=130米,BC=140米,AC=150米.市政府准备将其作为绿化用地,请你求出绿化用地的面积.
如图,三条公路的交叉地带是一个三角形,经测量这个三角形的三条边长分别是AB=130米,BC=140米,AC=150米.市政府准备将其作为绿化用地,请你求出绿化用地的面积.查看答案和解析>>
科目:初中数学 来源:学习周报 数学 北师大八年级版 2009-2010学年 第2期 总第158期 北师大版 题型:044
如图,三条公路的交叉地带是一个三角形,经测量这个三角形的三条边分别是
130米、140米、150米.市政府准备将其作为绿化用地,你能求出绿地用地的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,三条公路的交叉地带是一个三角形,经测量这个三角形的三条边长分别是:AB长130米,BC长140米,AC的长150米.市政府准备将其作为绿化用地,你能求出绿化用地的面积吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com