
【题目】为响应我市“中国梦”“宜宾梦”主题教育活动,某中学在全校学生中开展了以“中国梦我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
等级 | 频数 | 频率 |
一等奖 | a | 0.1 |
二等奖 | 10 | 0.2 |
三等奖 | b | 0.4 |
优秀奖 | 15 | 0.3 |
请你根据以上图表提供的信息,解答下列问题:
(1)a= , b= , n= .
(2)学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率.
【答案】
(1)5;20;144
(2)解:列表得:
A | B | C | 王 | 李 | |
A | ﹣ | AB | AC | A王 | A李 |
B | BA | ﹣ | BC | B王 | B李 |
C | CA | CB | ﹣ | C王 | C李 |
王 | 王A | 王B | 王C | ﹣ | 王李 |
李 | 李A | 李B | 李C | 李王 | ﹣ |
∵共有20种等可能的情况,恰好是王梦、李刚的有2种情况,
∴恰好选中王梦和李刚两位同学的概率P= ![]() =
= ![]()
【解析】解:(1)观察统计表知,二等奖的有10人,频率为0.2, 故参赛的总人数为10÷0.2=50人,
a=50×0.1=5人,b=50×0.4=20.
n=0.4×360°=144°,
故答案为:5,20,144;
(1)首先利用频数、频率之间的关系求得参赛人数,然后乘以一等奖的频率即可求得a值,乘以三等奖的频率即可求得b值,用三等奖的频率乘以360°即可求得n值;(2)列表后即可将所有情况全部列举出来,从而求得恰好抽中者两人的概率;


科目:初中数学 来源: 题型:
【题目】定义:如果两个一元一次方程的解互为相反数,我们就称这两个方程为“兄弟方程”.
如方程2x=4和3x+6=0为“兄弟方程”.
(1)若关于x的方程5x+m=0与方程2x﹣4=x+1是“兄弟方程”,求m的值;
(2)若两个“兄弟方程”的两个解的差为8,其中一个解为n,求n的值;
(3)若关于x的方程2x+3m﹣2=0和3x﹣5m+4=0是“兄弟方程”,求这两个方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,﹣2),且顶点在第三象限,设P=a﹣b+c,则P的取值范围是( ) 
A.﹣4<P<0
B.﹣4<P<﹣2
C.﹣2<P<0
D.﹣1<P<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知MN∥PQ,点B在MN上,点C在PQ上,点A在点B的左侧,点D在点C的右侧,∠ADC,∠ABC的平分线相交于点E(不与B,D点重合),∠CBN=110°.
(1)若∠ADQ=140°,写出∠BED的度数 (直接写出结果即可);
(2)若∠ADQ=m°,将线段AD沿DC方向平移,使点D移动到点C的左侧,其他条件不变,如图②所示,求∠BED的度数(用含m的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180° 时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.

(1)特例感知:在图2,图3中,△ABC与△DAE互为“顶补等腰三角形”,AM是“顶心距”。
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,ED=6时,AM的长为 。
(2)猜想论证:
在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明。

(3)拓展应用
如图4,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,CA=![]() ,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
①请在图中标出点P的位置,并描述出该点的位置为 ;
②直接写出△PBC的“顶心距”的长为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将从1开始的连续自然数按图规律排列:规定位于第3行,第2列的自然数10记为(3,2),自然数15记为(4,2)…….
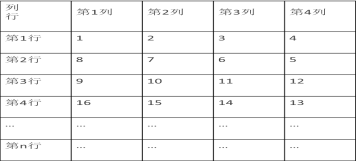
按此规律,回答下列问题:
(1)记为(6,3)表示的自然数是___________;
(2)自然数2018记为 __________;
(3)用一个正方形方框在第3列和第4列中任意框四个数,这四个数的和能为2018吗?如果能,求出框出的四个数中最小的数;如果不能,请写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题.
为促进学生健康成长,切实提高学生健康水平,某校为各班用400元购进若干体育用品,接着又用450元购进第二批体育用品,已知第二批所购体育用品数是第一批所购体育用品数的1.5倍,且每件体育用品的进价比第一批的进价少5元,求第一批体育用品每件的进价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com