
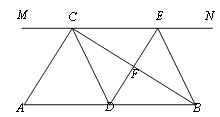
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时.
①求证:四边形BECD是菱形;
②当∠A为多少度时,四边形BECD是正方形?说明理由.
【答案】(1)证明见解析;(2)四边形BECD是菱形,理由见解析;(3)当∠A=45°时,四边形BECD是正方形,理由见解析.
【解析】试题分析:(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;(3)求出∠CDB=90°,再根据正方形的判定推出即可.
试题解析:(1)∵DE⊥BC, ∴∠DFB=90°, ∵∠ACB=90°, ∴∠ACB=∠DFB,
∴AC∥DE, ∵MN∥AB,即CE∥AD, ∴四边形ADEC是平行四边形, ∴CE=AD;
(2)四边形BECD是菱形, 理由是:∵D为AB中点, ∴AD=BD, ∵CE=AD,
∴BD=CE, ∵BD∥CE, ∴四边形BECD是平行四边形, ∵∠ACB=90°,D为AB中点,
∴CD=BD, ∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是: 解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°, ∴AC=BC, ∵D为BA中点, ∴CD⊥AB, ∴∠CDB=90°,
∵四边形BECD是菱形, ∴菱形BECD是正方形, 即当∠A=45°时,四边形BECD是正方形.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】一元二次方程x2-x+1=0的根的情况为( )
A. 有两个相等的实数根
B. 没有实数根
C. 有两个不相等的实数根
D. 有两个不相等的实数根,且两实数根和为1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式,能用平方差公式计算的是( )
A.(-a+b)(b-a)
B.(2x+1)(-2x-1)
C.(-5y+3)(5y+3)
D.(-2m+n)(2m-n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O1与⊙O2的圆心距O1O2=6cm,且两圆的半径满足一元二次方程x2-6x+8=0,则两圆的位置关系为 ( )
A. 外切 B. 内切 C. 外离 D. 相交
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果将三角形ABC三个顶点的横坐标都减2,纵坐标都加6,得到三角形A′B′C′,则三角形A′B′C′是由三角形ABC先向____平移____个单位长度,再向____平移____个单位长度得到.
查看答案和解析>>
科目:初中数学 来源: 题型:
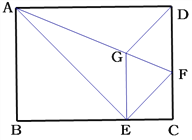
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG,GF,AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若ab=0,则点P(a,b)表示原点
B. 点(1,﹣a2)在第四象限
C. 已知点A(2,3)与点B(2,﹣3),则直线AB平行x轴
D. 坐标轴上的点不属于任何象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com