
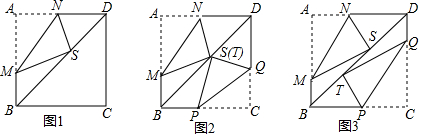
分析 (1)当点M与B重合时,∠AMN的值最小,此时∠AMN=$\frac{1}{2}$∠ABD=22.5°,当点N与D重合时,∠AMN的值最大,此时∠AMN=90°-22.5°=67.5°,由此即可解决问题;
(2)如图1中,AM=1时,作MK⊥BD于K.只要证明K与S重合即可解决问题;
(3)①如图2中,连接AS、CS分别交MN于G,交PQ于K.只要证明△MAG≌△PCK即可;
②如图3中,连接AS、CS分别交MN于G,交PQ于K.首先证明△ABS≌△CDT,推出AS=TC,再证明△MAG≌△QCK即可解决问题;
解答 解:(1)当点M与B重合时,∠AMN的值最小,此时∠AMN=$\frac{1}{2}$∠ABD=22.5°,
当点N与D重合时,∠AMN的值最大,此时∠AMN=90°-22.5°=67.5°,
故22.5°≤∠AMN≤67.5°.
(2)如图1中,AM=1时,作MK⊥BD于K.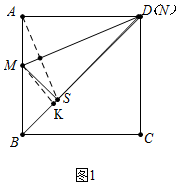
∵AB=1+$\sqrt{2}$,AM=MS=1,
∴BM=$\sqrt{2}$,
在Rt△BKM中,∵∠MBK=45°,BM=$\sqrt{2}$,
∴MK=BK=1,
∵MS=1,
∴S与K重合,
∴MS⊥BD,
∴此时N与D重合,∠ADM=∠MDB=22.5°,
∴∠AMN=67.5°.
(3)①如图2中,连接AS、CS分别交MN于G,交PQ于K.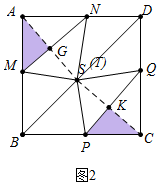
构建对称性可知,AS=SC,∠MAG=∠PCK,
∵AG=GS,SK=KC,
∴AG=CK,∵∠MGA=∠PKC=90°,
∴△MAG≌△PCK,
∴AM=PC.
②如图3中,连接AS、CS分别交MN于G,交PQ于K.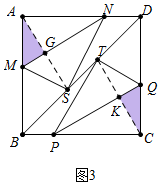
∵PQ∥MN,AS⊥MN,TC⊥PQ,
∴AS∥TC,
∵AB∥CD,
∴∠BAS=∠DCT,
∵∠ABS=∠CDT,AB=CD,
∵△ABS≌△CDT,
∴AS=TC,
∵AG=GS,TK=KC,
∴AG=CK,∵∠MGA=∠QKC=90°,
∴△MAG≌△QCK,
∴AM=QC.
点评 本题考查四边形综合题、轴对称变换、全等三角形的判定和性质、正方形的性质、等腰直角三角形的性质和判定等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
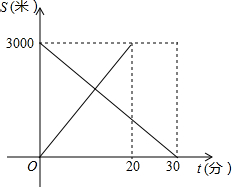 甲从A地出发,匀速步行到B地,同时,乙从B地出发,匀速步行到A地,甲乙两人与A地的距离S(米)与出发时间t(分钟)的关系如图:
甲从A地出发,匀速步行到B地,同时,乙从B地出发,匀速步行到A地,甲乙两人与A地的距离S(米)与出发时间t(分钟)的关系如图:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)请在如图的网格中建立适当的平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,-2);
(1)请在如图的网格中建立适当的平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,-2);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com