
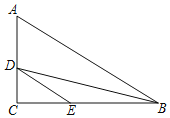
【题目】如图,△ABC中,∠C=90°,∠B=30°,AC=![]() ,D、E分别在边AC、BC上,CD=1,DE∥AB,将△CDE绕点C旋转,旋转后点D、E对应的点分别为D′、E′,当点E′落在线段AD′上时,连接BE′,此时BE′的长为( )
,D、E分别在边AC、BC上,CD=1,DE∥AB,将△CDE绕点C旋转,旋转后点D、E对应的点分别为D′、E′,当点E′落在线段AD′上时,连接BE′,此时BE′的长为( )
A.2![]() B.3
B.3![]() C.2
C.2![]() D.3
D.3![]()
【答案】B
【解析】
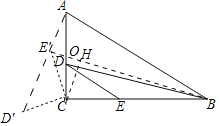
如图,作CH⊥BE′于H,设AC交BE′于O.首先证明∠CE′B=∠D′=60°,解直角三角形求出HE′,BH即可解决问题.
解:如图,作CH⊥BE′于H,设AC交BE′于O.
∵∠ACB=90°,∠ABC=30°,
∴∠CAB=60°,
∵DE∥AB,
∴![]() =
=![]() ,∠CDE=∠CAB=∠D′=60°
,∠CDE=∠CAB=∠D′=60°
∴![]() =
=![]() ,
,
∵∠ACB=∠D′CE′,
∴∠ACD′=∠BCE′,
∴△ACD′∽△BCE′,
∴∠D′=∠CE′B=∠CAB,
在Rt△ACB中,∵∠ACB=90°,AC=![]() ,∠ABC=30°,
,∠ABC=30°,
∴AB=2AC=2![]() ,BC=
,BC=![]() AC=
AC=![]() ,
,
∵DE∥AB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴CE=![]() ,
,
∵∠CHE′=90°,∠CE′H=∠CAB=60°,CE′=CE=![]()
∴E′H=![]() CE′=
CE′=![]() ,CH=
,CH=![]() HE′=
HE′=![]() ,
,
∴BH=![]() =
=![]() =
=![]()
∴BE′=HE′+BH=3![]() ,
,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,PA与⊙O相切于A点,点C是⊙O上的一点,且PC=PA.

(1)求证:PC是⊙O的切线;
(2)若∠BAC=45°,AB=4,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
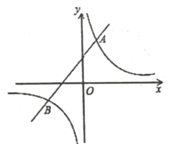
【题目】如图,已知反比例函数![]() 与一次函数
与一次函数![]() 的图象在第一象限相交于点
的图象在第一象限相交于点![]() .
.
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点![]() 的坐标,并根据图像写出使反比例函数的值大于一次函数的值的
的坐标,并根据图像写出使反比例函数的值大于一次函数的值的![]() 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
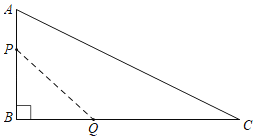
【题目】如图所示,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始,以2mm/S的速度沿边AB向B移动(不与点B重合),动点Q从点B开始,以4m/s的速度沿边BC向C移动(不与C重合),如果P、Q分别从A、B同时出发,设运动的时间为xs,四边形APQC的面积为ymm2.
(1)写出y与x之间的函数表达式;
(2)当x=2时,求四边形APQC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x(x﹣3)(0≤x≤3)的图象,记为C1,它与x轴交于点O,A1;将C1点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……若P(2020,m)在这个图象连续旋转后的所得图象上,则m=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
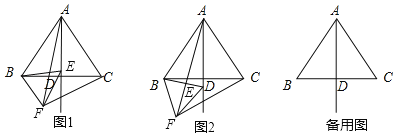
【题目】已知△ABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转60°得到BF,连接EF、CF、AF.
(1)如图1,当点E在线段AD上时,猜想∠AFC和∠FAC的数量关系;(直接写出结果)
(2)如图2,当点E在线段AD的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
(3)点E在直线AD上运动,当△ACF是等腰直角三角形时,请直接写出∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果按此速度增涨,该公司六月份的快递件数将达到多少万件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com