
【题目】为发展校园足球运动,我市城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打七折.
(1)求每套队服和每个足球的价格分别是多少元?
(2)若城区四校联合购买100套队服和a(a>10)个足球,请用含a的代数式分别表示出到甲商场和乙商场购买装备所花费用;
(3)在(2)的条件下,当a=65时,你认为到甲、乙哪家商场购买比较合算?说明理由.
【答案】(1)每套队服的价格是150元,每个足球的价格是100元;(2)到甲商场购买所需费用为(100a+14000)元;到乙商场购买所需费用为(70a+15000)元;(3)当a=65时,到乙商场购买比较合算.
【解析】
(1)设每个足球的价格是x元,则每套队服的价格是(x+50)元,根据两套队服与三个足球的费用相等,即可得出关于x的一元一次方程,解之即可得出结论;
(2)利用总价=单价×数量结合两商场的优惠方案,即可用含a的代数式表示出分别到甲、乙两商场购买所需费用;
(3)代入a=65可求出到两商场购买所需费用,比较后即可得出结论.
解:(1)设每个足球的价格是x元,则每套队服的价格是(x+50)元,
依题意,得:2(x+50)=3x,
解得:x=100,
∴x+50=150.
答:每套队服的价格是150元,每个足球的价格是100元.
(2)到甲商场购买所需费用为150×100+100(a﹣![]() )=100a+14000(元);
)=100a+14000(元);
到乙商场购买所需费用为150×100+0.7×100a=70a+15000(元).
(3)当a=65时,100a+14000=20500,70a+15000=19550,
∵20500>19550,
∴当a=65时,到乙商场购买比较合算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有三条长度均为a的线段,分别按以下要求画圆.
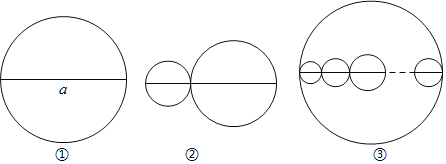
(1)如图①,以该线段为直径画一个圆,记该圆的周长为C1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C2,请指出C1和C2的数量关系,并说明理由;
(2)如图③,当a=11时,以该线段为直径画一个大圆,再在大圆内画若千小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为 .(直接填写答案,结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按如下规律摆放三角形:
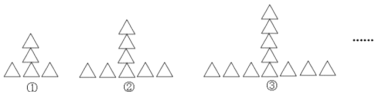
(1)图④中分别有多少个三角形?
(2)按上述规律排列下去,第n个图形中有多少个三角形?
(3)按上述规律排列下去,第2014个图形中有多少个三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015珠海)阅读材料:善于思考的小军在解方程组![]() 时,采用了一种“整体代换”的解法:将方程②变形:4x+10y+y=5 即2(2x+5y)+y=5③
时,采用了一种“整体代换”的解法:将方程②变形:4x+10y+y=5 即2(2x+5y)+y=5③
把方程①带入③得:2×3+y=5,∴y=﹣1
把y=﹣1代入①得x=4,∴方程组的解为![]() .
.
请你解决以下问题:(1)模仿小军的“整体代换”法解方程组![]() ;
;
(2)已知x,y满足方程组![]() .
.
(i)求![]() 的值;
的值;
(ii)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,抛物线y=-![]() x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP面积为S.当y≤3时,S随x变化的图象大致是( )
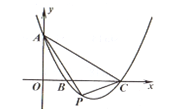
A. 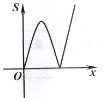 B.
B.  C.
C. 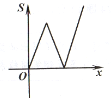 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表中的数据信息:

根据表中的信息判断,下列语句中正确的是( )
A.![]() 1.53
1.53
B.241的算术平方根比15.5小
C.根据表中数据的变化趋势,可以推断出16.12将比256增大3.17
D.只有3个正整数n满足15.7![]() 15.8
15.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化课改,落实立德树人目标,某学校设置了以下四门拓展性课程:A.数学思维,B.文学鉴赏,C.红船课程,D.3D打印,规定每位学生选报一门.为了解学生的报名情况,随机抽取了部分学生进行调查,并制作成如下两幅不完整的统计图,请回答下列问题:
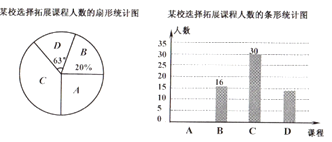
(1)求这次被调查的学生人数;
(2)请将条形统计图补充完整;
(3)假如全校有学生1000人,请估计选报“红船课程”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
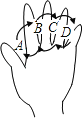
【题目】如图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即ABCDCBABC…的方式)从A开始数连续的正整数1,2,3,4…当数到11时,对应的字母是__.当字母C第2n﹣1次出现时(n为正整数),恰好数到的数是__(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com