
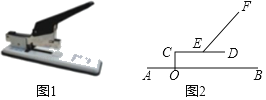
����Ŀ������������ƶ������а塢ѹ��������������λ�����ɣ���ͼ1��һ̨������ˮƽ�����ϵĴ��Ͷ�������������������ͼ2��ʾ�ļ���ͼ�Σ���ѹ����EF�Ķ˵�E�̶��ڶ�λ��CD���е㴦����ʹ�ù����У���D�͵�F��ѹ��������λ���Ƶ�C��ת��CO��AB�ڵ�O��CD��12cm����CF������FED��45������FCD��30����
��1����FC�ij���
��2����OC��2cm����ʹ�ù����У�����D���ڵ���AB��ʱ�������CD��AB�ļнǼ���F�˶���·��֮�����������ȷ��0.1cm���ο����ݣ�sin9.6���0.17���С�3.14��![]() 1.732��
1.732��
���𰸡���1��CF��16.4cm����2��CD��AB�ļн�Ϊ9.6������F�˶���·�߳�Ϊ2.7cm��
��������
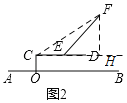
��1������CF������F��FH��CE���ӳ����ڵ�H����EH��FH��x��Ȼ�����tan��FCH��![]() ��
��![]() ��
��![]() ���������x��ֵ��
���������x��ֵ��
��2������������Ǻ����Ķ�������sin��CDA��![]() ��0��17���Ӷ����������D���ڵ���AB��ʱ��CD��AB�ļн�Ϊ9��6���������ݻ�����ʽ��������𰸣�
��0��17���Ӷ����������D���ڵ���AB��ʱ��CD��AB�ļн�Ϊ9��6���������ݻ�����ʽ��������𰸣�
��1������CF������F��FH��CE���ӳ����ڵ�H����ͼ2��
�ߡ�FEH��45������FHC��90����
��EH��FH��x��
�ߡ�FCH��30����
��tan��FCH��![]() ��
��![]() ��
��![]() ��
��
��x��3![]() +3��
+3��
��CF��2x��6![]() +6��16��4cm��
+6��16��4cm��
��2����ʹ�ù����У�CD��AB�ļн�Ϊ��
sin��CDA��![]() ��0��17��
��0��17��
��sin9��6���0��17��
�൱��D���ڵ���AB��ʱ��CD��AB�ļн�Ϊ9��6����
�ߵ�F���˶�·������CΪԲ�ģ�CFΪ�뾶��Բ���ϣ�
�ҵ�D���ڵ���AB��ʱ����F�Ƶ�C��ת��9��6����
��l��![]() ��2��7cm��
��2��7cm��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������л������Ͼ�����˾����һ�ֻ���ԭ������ǧ�ˣ��۸�Ϊÿǧ ��30Ԫ����۲��Ź涨�����۵��۲�����ÿǧ��60Ԫ��������ÿǧ��30Ԫ�����г����鷢�֣���������y��ǧ�ˣ������۵���x��Ԫ����һ�κ������ҵ�x=60ʱ ��y=80��x=50ʱ��y=100�������۹����У�ÿ�컹Ҫ֧����������450Ԫ��
��1����3�֣����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����3�֣���ù�˾���۸�ԭ���ջ���w��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��3����4�֣������۵���Ϊ����Ԫʱ���ù�˾�ջ�������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Զ�˶�Ա������ѵ��Ч�����в��ԣ�6����Զ�ijɼ����£�7.5��7.7��7.6��7.7��7.9��7.8����λ��m�������γɼ���ƽ����Ϊ7.7m������Ϊ![]() �������������һ�Σ��ɼ�Ϊ7.7m����������7����Զ�ɼ��ķ���_____���������������������������С������
�������������һ�Σ��ɼ�Ϊ7.7m����������7����Զ�ɼ��ķ���_____���������������������������С������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ������A��1��0����B��0��3�����䶥��ΪD����PΪ����������һ�㣬��λ�������߶Գ����Ҳ࣬��PH�ͶԳ��ᣬ����ΪH������DPH����AOB����
������A��1��0����B��0��3�����䶥��ΪD����PΪ����������һ�㣬��λ�������߶Գ����Ҳ࣬��PH�ͶԳ��ᣬ����ΪH������DPH����AOB����
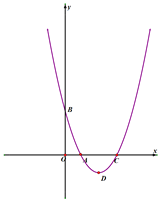
��1���������ߵĽ���ʽ
��2�����P������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
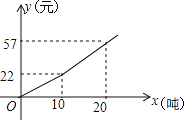
����Ŀ��Ϊ���������Լ��ˮ��ij������ˮ��˾���ֶ��շѱ��շѣ���ͼ��ӳ����ÿ����ˮ��y��Ԫ������ˮ��x���֣�֮��ĺ�����ϵ
��1��С������·���ˮ8�֣�Ӧ��ˮ��_____Ԫ��
��2���������ֶ��շѱ���С����������·ݷֱ�ˮ��36Ԫ��19.8Ԫ�������·ݱ����·ݽ�Լ��ˮ���ٶ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c�ĶԳ���Ϊֱ��x=��1������ͼ����ͼ��ʾ�������ж��У�
��abc��0��
��b2��4ac��0��
��9a��3b+c=0��
�����㣨��0.5��y1��������2��y2�������������ϣ���y1��y2��
��5a��2b+c��0��
������ȷ�ĸ����У�������
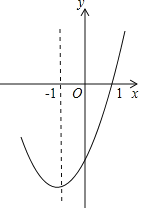
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ� ��
A.ͬһƽ���ڣ���һ������ֻ��һ��ֱ������ֱ֪��ƽ��
B.���ŷֱ������Ρ��ȱ������Ρ�Բ�Ŀ�Ƭ�����������ȡһ�ţ�ǡ�ó鵽���ĶԳ�ͼ�ο�Ƭ�ĸ�����![]()
C.һ��Ա�ƽ�У�һ��Ա���ȵ��ı�����ƽ���ı���
D.��![]() ʱ������
ʱ������![]() �ķ���
�ķ���![]() ��ʵ����
��ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
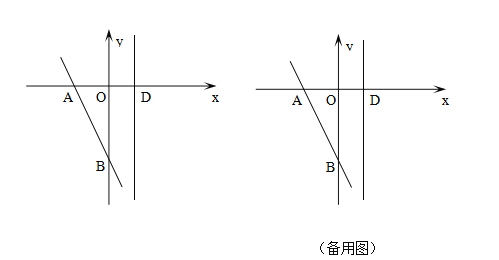
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y��kx+b��ͼ����A��-2��0����B��0��-2![]() ������D��1��0����ƽ����y���ֱ��l��
������D��1��0����ƽ����y���ֱ��l��
��1�� ��һ�κ���y��kx+b�ı���ʽ��
��2����PΪy���ϵ�һ�����㣬����PD����![]() ����СֵΪ____ ____.
����СֵΪ____ ____.
��3��M��s��t��Ϊֱ��l�ϵ�һ�����㣬��ƽ���ڴ��ڵ�N��ʹ��A��B��M��NΪ������ı���Ϊ���Σ�����M��N������ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������ѧ��ҵ��������ҵ,ij��������̨���������:������Э��,������ҵ���ɱ����ṩ��Ʒ����ѧ��ҵ����������,�ɱ����������֮��IJ���������е������������������Ͷ�����۱���������һ�����ͽ��ܵƣ���֪���ֽ��ܵƵijɱ���Ϊÿ��![]() Ԫ,������Ϊÿ��
Ԫ,������Ϊÿ��![]() Ԫ,ÿ��������
Ԫ,ÿ��������![]() �����������۵���
�����������۵���![]() ��Ԫ��֮��Ĺ�ϵ��������һ�κ���:
��Ԫ��֮��Ĺ�ϵ��������һ�κ���:![]() ��
��
��1�������ڿ�ʼ��ҵ�ĵ�һ���½����۵��۶�Ϊ![]() Ԫ,��ô���������Ϊ���е����ܲ��Ϊ����Ԫ?
Ԫ,��ô���������Ϊ���е����ܲ��Ϊ����Ԫ?
��2����������õ�����Ϊ![]() ��Ԫ��,�����۵��۶�Ϊ����Ԫʱ,ÿ�¿ɻ���������?
��Ԫ��,�����۵��۶�Ϊ����Ԫʱ,ÿ�¿ɻ���������?
��3����۲��Ź涨,���ֽ��ܵƵ����۵��۲��ø���![]() Ԫ�����������Ҫÿ�»�õ�������
Ԫ�����������Ҫÿ�»�õ�������![]() Ԫ,��ô����Ϊ���е����ܲ������Ϊ����Ԫ?
Ԫ,��ô����Ϊ���е����ܲ������Ϊ����Ԫ?
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com