�⣺��1����������ABCD�ı߳�Ϊ12����S
������ABCD=12
2=144��
��O��AD���е㣬��OA=OD=6��
�٣���t=4ʱ����ͼ1�٣�
��AP=2��4=8��OA=6��
��S
��OAP=

��AP��OA=24��
��y=S
������ABCD-S
��OAP=144-24=120��
����t=8ʱ����ͼ1�ڣ�
��AB+BP=2��8=16��AB=12��
��BP=4����CP=12-4=8��
��y=

��OD+CP����CD=

����6+8����12=84��
����t=14ʱ����ͼ1�ۣ�
��AB+BC+CP=2��14=28��AB=BC=CD=12��
��DP=12��3-28=8��
��y=S
��ODP=

��DP��OD=24��
�ڷ����������
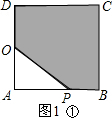
����0��t��6ʱ����P�ڱ�AB�ϣ���ͼ1�٣�
��AP=2t��OA=6��
��S
��OAP=

��AP��6=6t��
��y=S
������ABCD-S
��OAP=144-6t��
����6��t��12ʱ����P�ڱ�BC�ϣ���ͼ1�ڣ�
��AB+BP=2t��AB=CD=12��
��CP=24-2t��
��y=

��OD+CP����CD=

����6+24-2t����12=180-12t��
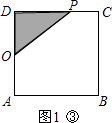
����12��t��18ʱ����P�ڱ�CD�ϣ���ͼ1�ۣ�
��AB+BC+CP=2t��AB=BC=CD=12��
��DP=36-2t��
��y=S
��ODP=

��DP��OD=108-6t��
���Ͽ�֪��y=
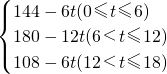
��
��2���١�t=0ʱ��S=S
������ABCD=16��
��������ABCD�ı߳�=4��
��t=4ʱ��S=0��
��P��Q�����ڵ�4��������
�ڡ�S��t�ĺ���ͼ����5����ɣ�
��P��Q������C�㣬
��ʱ����ͬʱ���ٶ�֮�ȵ���·��֮�ȣ�����P�˶���·��=��Q�˶���·�̵�2����
���P���ٶ�=��Q���ٶȵ�2����
���Q���ٶ�Ϊa��λ����/�룬���P���ٶ�Ϊ2a��λ����/�룮
��t=4ʱ��P��Q������C�㣬������ABCD�ı߳�Ϊ4��
��4��a+2a��=4��3��
��a=1��

�ʵ�P���ٶ�Ϊ2��λ����/�룬��Q���ٶ�Ϊ1��λ����/�룻
�ۡ�������ABCD�ı߳�Ϊ4����S
������ABCD=16��
��O��AD���е㣬��OA=OD=2��
��t��ʱ��������ABCD���POQ��������Ե���ڲ����ص����ֵ����S����9��
����������������ۣ�
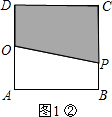
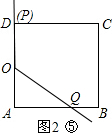
����0��t��2ʱ����P�ڱ�AB�ϣ���Q�ڱ�CD�ϣ���ͼ2�٣�
��AP=2t��DQ=t��OA=OD=2��
��S=S
������ABCD-S
��OAP-S
��ODQ=16-2t-t=16-3t��
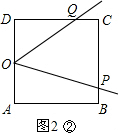
��16-3t=9��
���t=

���������⣬��ȥ����
����2��t��4ʱ����P�ڱ�BC�ϣ���Q�ڱ�CD�ϣ���ͼ2�ڣ�
��AB+BP=2t��AB=4����BP=2t-4��
��DQ=t��OA=OD=2��
��S=S
������ABCD-S
����OABP-S
��ODQ=16-

����2t-4+2����4-

��2t=20-5t��
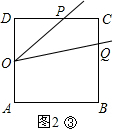
��20-5t=9��
���t=
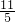
��
����4��t��6ʱ����P�ڱ�CD�ϣ���Q�ڱ�CB�ϣ���ͼ2�ۣ�
��AB+BC+CP=2t��AB=BC=CD=4����DP=12-2t��
��DC+CQ=t����BQ=8-t��
��S=S
������ABCD-S
����OABQ-S
��ODP=16-

����2+8-t����4-

��2����12-2t��=4t-16��
��4t-16=9��
���t=

���������⣬��ȥ����
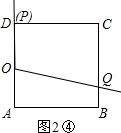
��������6��t��8ʱ����P��D���غϣ���Q�ڱ�CB�ϣ���ͼ2�ܣ�
��DC+CQ=t��DC=4����CQ=t-4��
��S=S
����ODCQ=

����t-4+2����4=2t-4��
��2t-4=9��
���t=

��
��������8��t��12ʱ����P��D���غϣ���Q�ڱ�AB�ϣ���ͼ2�ݣ�
��DC+CB+BQ=t��DC=CB=AB=4����AQ=12-t��
��S=S
������ABCD-S
��OAQ=16-

��2����12-t��=4+t��
��4+t=9��
���t=5���������⣬��ȥ����
���Ͽ�֪����tΪ
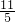
��

ʱ���ص��������S����9��
�ʴ�Ϊ����2����4��4����2��1��
��������1��������������ABCD�ı߳�Ϊ12����P��A�������A��B��C��D��·�������˶������˶��ٶ�Ϊ2��λ����/�룬��������ȷ��t=4��8��14ʱP�����ڵ�λ�ã�Ȼ������ص����ֵ���״��������Ӧ�������ʽ���������Ӧ��yֵ��
�����ڵ�P��ÿһ�������˶���ʱ��Ϊ6�룬���Է���������������ۣ�����0��t��6������P�ڱ�AB��ʱ������6��t��12������P�ڱ�BC��ʱ������12��t��18������P�ڱ�CD��ʱ�����ÿһ������������Ը����ص����ֵ���״��������Ӧ�������ʽ�����Ӧ��y����t�ĺ�������ʽ��
��2��������t=0ʱ����P��A���غϣ���Q��D���غϣ���ʱS=16=S
������ABCD�����Եó������εı߳�=4������ΪS=0��P��Q��������������ʱ��Ӧ��t=4������P��Q�����ڵ�4��������
������S��t�ĺ���ͼ����5����ɣ���ֻ�е�P��Q������C��ʱͼ���Ϊ5�Σ��������ͼ���Ϊ6�Σ�����P��Q������C�㣬����ʱ����ͬʱ���ٶ�֮�ȵ���·��֮�ȵó���P���ٶ��ǵ�Q���ٶȵ�2��������t=4ʱ��P��Q�����˶���·��֮�͵���AB+BC+CD���ݴ��г����̣���⼴�ɣ�
����t��ʱ��������ABCD���POQ��������Ե���ڲ����ص����ֵ����S����9������P��Q���㶼�ڱ߳�Ϊ4�������ε��������˶�����P��ÿһ�������˶���ʱ����2�룬��Q��ÿһ�������˶���ʱ����4�룬���Է���������������ۣ�����0��t��2������P�ڱ�AB�ϣ���Q�ڱ�CD��ʱ������2��t��4������P�ڱ�BC�ϣ���Q�ڱ�CD��ʱ������4��t��6������P�ڱ�CD�ϣ���Q�ڱ�CB��ʱ����������6��t��8������P��D���غϣ���Q�ڱ�CB��ʱ����������8��t��12������P��D���غϣ���Q�ڱ�AB��ʱ�����ÿһ������������Ը����ص����ֵ���״��������Ӧ�������ʽ����ú�t�Ĵ���ʽ��ʾS��ʽ�ӣ�Ȼ����S=9���ⷽ�̣���������tֵ�ڶ�Ӧ�ķ�Χ�ڣ���������⣻�����������⣬��ȥ��
���������⿼����Ƕ�������ĺ���ͼ����һ�κ����ۺ��⣬�ۺ��Ժ�ǿ���ѶȽϴ��ݶ����˶����ٶȼ��˶�·��ȷ�������λ���ǽ���Ĺؼ������÷������۵�˼����ȷ���з����DZ�����ѵ㣮


 �⣺��1����������ABCD�ı߳�Ϊ12����S������ABCD=122=144��
�⣺��1����������ABCD�ı߳�Ϊ12����S������ABCD=122=144�� ��AP��OA=24��
��AP��OA=24�� ��OD+CP����CD=
��OD+CP����CD= ����6+8����12=84��
����6+8����12=84�� ��AB+BC+CP=2��14=28��AB=BC=CD=12��
��AB+BC+CP=2��14=28��AB=BC=CD=12�� ��DP��OD=24��
��DP��OD=24�� ��AP��6=6t��
��AP��6=6t�� ��OD+CP����CD=
��OD+CP����CD= ����6+24-2t����12=180-12t��
����6+24-2t����12=180-12t�� ����12��t��18ʱ����P�ڱ�CD�ϣ���ͼ1�ۣ�
����12��t��18ʱ����P�ڱ�CD�ϣ���ͼ1�ۣ� ��DP��OD=108-6t��
��DP��OD=108-6t��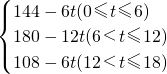 ��
�� �ʵ�P���ٶ�Ϊ2��λ����/�룬��Q���ٶ�Ϊ1��λ����/�룻
�ʵ�P���ٶ�Ϊ2��λ����/�룬��Q���ٶ�Ϊ1��λ����/�룻 ��16-3t=9��
��16-3t=9�� ���������⣬��ȥ����
���������⣬��ȥ���� ����2t-4+2����4-
����2t-4+2����4- ��2t=20-5t��
��2t=20-5t�� ��20-5t=9��
��20-5t=9��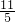 ��
�� ����2+8-t����4-
����2+8-t����4- ��2����12-2t��=4t-16��
��2����12-2t��=4t-16�� ��4t-16=9��
��4t-16=9�� ���������⣬��ȥ����
���������⣬��ȥ���� ����t-4+2����4=2t-4��
����t-4+2����4=2t-4�� ���t=
���t= ��
�� ��2����12-t��=4+t��
��2����12-t��=4+t��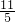 ��
�� ʱ���ص��������S����9��
ʱ���ص��������S����9��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
 ��֪����ͼ��ʾ����������ABCD�У�EΪAD���е㣬FΪDC�ϵ�һ�㣬��DF=
��֪����ͼ��ʾ����������ABCD�У�EΪAD���е㣬FΪDC�ϵ�һ�㣬��DF= 18����������ABCD�У���G��BC������һ�㣬����AG����B��D����ֱ���BE��AG��DF��AG������ֱ�ΪE��F���㣬��֤����ADF�ա�BAE��
18����������ABCD�У���G��BC������һ�㣬����AG����B��D����ֱ���BE��AG��DF��AG������ֱ�ΪE��F���㣬��֤����ADF�ա�BAE��
 ��ͼ����������ABCD�У�P��CD��һ�㣬��AP=BC+CP��QΪCD�е㣬��֤����BAP=2��QAD��
��ͼ����������ABCD�У�P��CD��һ�㣬��AP=BC+CP��QΪCD�е㣬��֤����BAP=2��QAD��