
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
 一艘船由O港出发,先沿北偏东30°方向航行至A处,折向正西方向航行至B处,再沿南偏东60°方向航行,恰好回到O港,历时2.5h,假设船以匀速行驶,问这艘船向正西方向行驶了多少时间?(要求画出航线示意图,结果精确到分)
一艘船由O港出发,先沿北偏东30°方向航行至A处,折向正西方向航行至B处,再沿南偏东60°方向航行,恰好回到O港,历时2.5h,假设船以匀速行驶,问这艘船向正西方向行驶了多少时间?(要求画出航线示意图,结果精确到分)查看答案和解析>>
科目:初中数学 来源: 题型:
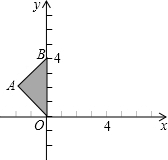 在平面直角坐标系中,等腰Rt△OAB斜边OB在y轴上,且OB=4.
在平面直角坐标系中,等腰Rt△OAB斜边OB在y轴上,且OB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com