
ЁОЬтФПЁПШчЭМЂйЃЌОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() Дг
Дг![]() ДІПЊЪМАДЫГЪБеыЗНЯђа§зЊЃЌ
ДІПЊЪМАДЫГЪБеыЗНЯђа§зЊЃЌ![]() НЛБп
НЛБп![]() ЃЈЛђ
ЃЈЛђ![]() ЃЉгкЕу
ЃЉгкЕу![]() ЃЌ
ЃЌ![]() НЛБп
НЛБп![]() ЃЈЛђ
ЃЈЛђ![]() ЃЉгкЕу
ЃЉгкЕу![]() .ЕБ
.ЕБ![]() а§зЊжС
а§зЊжС![]() ДІЪБЃЌ
ДІЪБЃЌ![]() ЕФа§зЊЫцМДЭЃжЙ.
ЕФа§зЊЫцМДЭЃжЙ.
ЃЈ1ЃЉЬиЪтЧщаЮЃКШчЭМЂкЃЌЗЂЯжЕБ![]() Й§Еу
Й§Еу![]() ЪБЃЌ
ЪБЃЌ![]() вВЧЁКУЙ§Еу
вВЧЁКУЙ§Еу![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЪЧЗёгы
ЪЧЗёгы![]() ЯрЫЦЃПВЂЫЕУїРэгЩЃЛ
ЯрЫЦЃПВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉРрБШЬНОПЃКШчЭМЂлЃЌдка§зЊЙ§ГЬжаЃЌ![]() ЕФжЕЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГіИУЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЕФжЕЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГіИУЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЭиеЙбгЩьЃКЩш![]() ЪБЃЌ
ЪБЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЪдгУКЌ
ЃЌЪдгУКЌ![]() ЕФДњЪ§ЪНБэЪО
ЕФДњЪ§ЪНБэЪО![]() ЃЛ
ЃЛ
Ђйдка§зЊЙ§ГЬжаЃЌШє![]() ЪБЃЌЧѓЖдгІЕФ
ЪБЃЌЧѓЖдгІЕФ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
Ђкдка§зЊЙ§ГЬжаЃЌЕБ![]() ЕФУцЛ§ЮЊ4.2ЪБЃЌЧѓЖдгІЕФ
ЕФУцЛ§ЮЊ4.2ЪБЃЌЧѓЖдгІЕФ![]() ЕФжЕ.
ЕФжЕ.
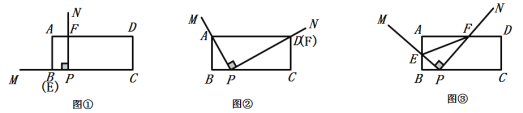
ЁОД№АИЁПЃЈ1ЃЉЯрЫЦЃЛЃЈ2ЃЉЖЈжЕЃЌ![]() ЃЛЃЈ3ЃЉЂй2ЃЌЂк
ЃЛЃЈ3ЃЉЂй2ЃЌЂк![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЁАСННЧЯрЕШЕФСНИіШ§НЧаЮЯрЫЦЁБМДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉгЩ![]() ЕУГі
ЕУГі![]() ЃЌгж
ЃЌгж![]() ЮЊЖЈжЕЃЌМДПЩЕУГіД№АИЃЛ
ЮЊЖЈжЕЃЌМДПЩЕУГіД№АИЃЛ
ЃЈ3ЃЉЯШЩш![]() НсКЯ
НсКЯ![]() ЕУГі
ЕУГі
![]() ЂйНЋt=1ДњШы
ЂйНЋt=1ДњШы![]() жаЧѓНтМДПЩЕУГіД№АИЃЛ
жаЧѓНтМДПЩЕУГіД№АИЃЛ
ЂкНЋs=4.2ДњШы![]() жаЧѓНтМДПЩЕУГіД№АИ.
жаЧѓНтМДПЩЕУГіД№АИ.
ЃЈ1ЃЉЯрЫЦ
РэгЩЃКЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ
дка§зЊЙ§ГЬжа![]() ЕФжЕЮЊЖЈжЕЃЌ
ЕФжЕЮЊЖЈжЕЃЌ
РэгЩШчЯТЃКЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЁп
ЃЌЁп![]() ЃЌ
ЃЌ
![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЁпЫФБпаЮ![]() ЮЊОиаЮЃЌЁрЫФБпаЮ
ЮЊОиаЮЃЌЁрЫФБпаЮ![]() ЮЊОиаЮЃЌ
ЮЊОиаЮЃЌ
Ёр![]()
Ёр![]()
МДдка§зЊЙ§ГЬжаЃЌ![]() ЕФжЕЮЊЖЈжЕЃЌ
ЕФжЕЮЊЖЈжЕЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃК![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]()
![]()
МДЃК![]() ЃЛ
ЃЛ
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФУцЛ§
ЕФУцЛ§![]() ЃЌ
ЃЌ
ЂкЕБ![]() ЪБЃЌЁр
ЪБЃЌЁр![]()
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЁрЕБ![]() ЕФУцЛ§ЮЊ4.2ЪБЃЌ
ЕФУцЛ§ЮЊ4.2ЪБЃЌ![]() ЃЛ
ЃЛ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧаЁУїЭЌбЇЩшМЦЕФЁАЙ§дВЭтвЛЕузїдВЕФЧаЯпЁБЕФГпЙцзїЭМЕФЙ§ГЬ.
вбжЊЃКШчЭМ1ЃЌ![]() КЭ
КЭ![]() ЭтЕФвЛЕу
ЭтЕФвЛЕу![]() .
.

ЧѓзїЃКЙ§Еу![]() зї
зї![]() ЕФЧаЯп.
ЕФЧаЯп.
зїЗЈЃКШчЭМ2ЃЌ

ЂйСЌНг![]() ЃЛ
ЃЛ
ЂкзїЯпЖЮ![]() ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп![]() ЃЌжБЯп
ЃЌжБЯп![]() НЛ
НЛ![]() гк
гк![]() ЃЛ
ЃЛ
ЂлвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖзїдВЃЌНЛ
ЮЊАыОЖзїдВЃЌНЛ![]() гкЕу
гкЕу![]() КЭ
КЭ![]() ЃЛ
ЃЛ
ЂмзїжБЯп![]() КЭ
КЭ![]() .
.
дђ![]() ЃЌ
ЃЌ![]() ОЭЪЧЫљЧѓзїЕФ
ОЭЪЧЫљЧѓзїЕФ![]() ЕФЧаЯп.
ЕФЧаЯп.
ИљОнЩЯЪізїЭМЙ§ГЬЃЌЛиД№ЮЪЬтЃК
ЃЈ1ЃЉгУжБГпКЭдВЙцЃЌВЙШЋЭМ2жаЕФЭМаЮЃЛ
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУїЃК
жЄУїЃКСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁпгЩзїЭМПЩжЊ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ
Ёр![]() ЃЈ______ЃЉЃЈЬювРОнЃЉЃЌ
ЃЈ______ЃЉЃЈЬювРОнЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гжЁп![]() КЭ
КЭ![]() ЪЧ
ЪЧ![]() ЕФАыОЖЃЌ
ЕФАыОЖЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ОЭЪЧ
ОЭЪЧ![]() ЕФЧаЯпЃЈ______ЃЉЃЈЬювРОнЃЉ.
ЕФЧаЯпЃЈ______ЃЉЃЈЬювРОнЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
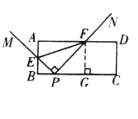
ЁОЬтФПЁПШчЭМЃЌ![]() КЭ
КЭ![]() ЖМЪЧЕШБпШ§НЧаЮЃЌЧвЕуAЁЂCЁЂEдкЭЌвЛжБЯпЩЯЃЌ
ЖМЪЧЕШБпШ§НЧаЮЃЌЧвЕуAЁЂCЁЂEдкЭЌвЛжБЯпЩЯЃЌ![]() гы
гы![]() ЁЂ
ЁЂ![]() ЗжБ№НЛгкЕуFЁЂMЃЌ
ЗжБ№НЛгкЕуFЁЂMЃЌ![]() гы
гы![]() НЛгкЕуNЃЎЯТСаНсТле§ШЗЕФЪЧ_______ЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉЃЎ
НЛгкЕуNЃЎЯТСаНсТле§ШЗЕФЪЧ_______ЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉЃЎ
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]()

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпy1=Љ2xОЙ§ЕуPЃЈЉ2ЃЌaЃЉЃЌЕуPЙигкyжсЕФЖдГЦЕуPЁфдкЗДБШР§КЏЪ§y2=![]() ЃЈkЁй0ЃЉЕФЭМЯѓЩЯЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓЩЯЃЎ
ЃЈ1ЃЉЧѓЕуPЕФзјБъЃЛ
ЃЈ2ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЌВЂжБНгаДГіЕБy2ЃМ2ЪБздБфСПxЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
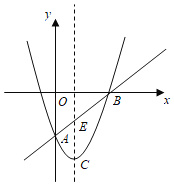
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊХзЮяЯп
жаЃЌвбжЊХзЮяЯп![]() гыжБЯп
гыжБЯп![]() ЖМОЙ§
ЖМОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЃЌИУХзЮяЯпЕФЖЅЕуЮЊCЃЎ
СНЕуЃЌИУХзЮяЯпЕФЖЅЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпКЭжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшжБЯп![]() гыИУХзЮяЯпЕФЖдГЦжсНЛгкЕуEЃЌдкЩфЯп
гыИУХзЮяЯпЕФЖдГЦжсНЛгкЕуEЃЌдкЩфЯп![]() ЩЯЪЧЗёДцдквЛЕуMЃЌЙ§MзїxжсЕФДЙЯпНЛХзЮяЯпгкЕуNЃЌЪЙЕуMЁЂNЁЂCЁЂEЪЧЦНааЫФБпаЮЕФЫФИіЖЅЕуЃПШєДцдкЃЌЧѓЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЩЯЪЧЗёДцдквЛЕуMЃЌЙ§MзїxжсЕФДЙЯпНЛХзЮяЯпгкЕуNЃЌЪЙЕуMЁЂNЁЂCЁЂEЪЧЦНааЫФБпаЮЕФЫФИіЖЅЕуЃПШєДцдкЃЌЧѓЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩшЕуPЪЧжБЯп![]() ЯТЗНХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЕБ
ЯТЗНХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЕБ![]() УцЛ§зюДѓЪБЃЌЧѓЕуPЕФзјБъЃЌВЂЧѓ
УцЛ§зюДѓЪБЃЌЧѓЕуPЕФзјБъЃЌВЂЧѓ![]() УцЛ§ЕФзюДѓжЕЃЎ
УцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
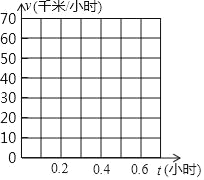
ЁОЬтФПЁПФГЬьЩЯЮч7ЃК30ЃЌаЁЗМдкМвЭЈЙ§ЕЮЕЮДђГЕШэМўДђГЕЧАЭљЖЏГЕеОДюГЫЕБЬьЩЯЮч8ЃК30ЕФЖЏГЕЃЎМЧЦћГЕЕФааЪЛЪБМфЮЊtаЁЪБЃЌааЪЛЫйЖШЮЊvЧЇУз/аЁЪБЃЈЦћГЕааЪЛЫйЖШВЛГЌЙ§60ЧЇУз/аЁЪБЃЉЃЎИљОнОбщЃЌvЃЌtЕФвЛзщЖдгІжЕШчЯТБэЃК
VЃЈЧЇУз/аЁЪБЃЉ | 20 | 30 | 40 | 50 | 60 |
TЃЈаЁЪБЃЉ | 0.6 | 0.4 | 0.3 | 0.25 | 0.2 |
ЃЈ1ЃЉИљОнБэжаЕФЪ§ОнУшЕуЃЌЧѓГіЦНОљЫйЖШvЃЈЧЇУз/аЁЪБЃЉЙигкааЪЛЪБМфtЃЈаЁЪБЃЉЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєаЁЗМДгПЊЪМДђГЕЕНЩЯГЕгУСЫ10ЗжжгЃЌаЁЗМЯыдкЖЏГЕГіЗЂЧААыаЁЪБЕНДяЖЏГЕеОЃЌШєЦћГЕЕФЦНОљЫйЖШЮЊ32ЧЇУз/аЁЪБЃЌаЁЗМФмЗёдкдЄЖЈЕФЪБМфФкЕНДяЖЏГЕеОЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЦћГЕЕНДяЖЏГЕеОЕФааЪЛЪБМфtТњзу0.3ЃМtЃМ0.5ЃЌЧѓЦНОљЫйЖШvЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЮЊСЫПЊЗЂРћгУКЃбѓзЪГЧЃЌФГПБВтЗЩЛњВтСПвЛЕКгьСНЖЫAЃЌBЕФОрИпЃЌЗЩЛњдкОрКЃЦНУцДЙжБИпЖШЮЊ100mЕФЕуCДІВтЕУЖЫЕуAЕФИЉНЧЮЊ60ЁуЃЌШЛКѓбизХЦНаагкABЕФЗНЯђЫЎЦНЗЩаа500mЃЌдкЕуDВтЕУЖЫЕуBЕФИЉНЧЮЊ45ЁуЃЌдђЕКгьСНЖЫAЃЌBЕФОрРыЮЊ___________.ЃЈНсЙћБЃСєИљКХЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкТЅABгыТЅCDжЎМфгавЛЦьИЫEFЃЌДгABЖЅВПAЕуДІОЙ§ЦьИЫЖЅВПEЕуЧЁКУПДЕНТЅCDЕФЕзВПDЕуЃЌЧвИЉНЧЮЊ45ЁуЃЌДгТЅCDЖЅВПCЕуДІОЙ§ЦьИЫЖЅВПEЕуЧЁКУПДЕНТЅABЕФGЕуЃЌBG=1УзЃЌЧвИЉНЧЮЊ30ЁуЃЌвбжЊТЅABИп20УзЃЌЧѓЦьИЫEFЕФИпЖШЃЎЃЈНсЙћОЋШЗЕН1УзЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
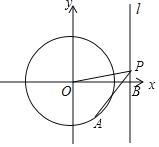
ЁОЬтФПЁПвбжЊЕуAЪЧдВаФЮЊзјБъдЕуOЧвАыОЖЮЊ3ЕФдВЩЯЕФЖЏЕуЃЌОЙ§ЕуBЃЈ4ЃЌ0ЃЉзїжБЯпlЁЭxжсЃЌЕуPЪЧжБЯпlЩЯЕФЖЏЕуЃЌШєЁЯOPAЃН45ЁуЃЌдђЁїBOPЕФУцЛ§ЕФзюДѓжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com