
 上.
上. 与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
 ,将其代入直线
,将其代入直线 中,即可求得点D的坐标,易知四边形ABDC是菱形,根据菱形的边长为2,以及点D的坐标,即可确定出其他三点的坐标.
中,即可求得点D的坐标,易知四边形ABDC是菱形,根据菱形的边长为2,以及点D的坐标,即可确定出其他三点的坐标.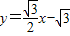 的解析式,易求得点P的坐标,而A、B的坐标在(1)题已经求得,即可利用待定系数法求出该抛物线的解析式.
的解析式,易求得点P的坐标,而A、B的坐标在(1)题已经求得,即可利用待定系数法求出该抛物线的解析式.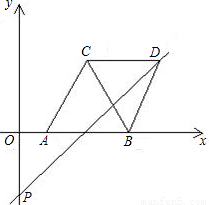 解:(1)依题意,四边形ABDC为菱形,
解:(1)依题意,四边形ABDC为菱形, ;
; ,
, 上,
上, ,
, ;
; ,抛物线过A、B、P三点,
,抛物线过A、B、P三点,
 ;
; .(6分)
.(6分) =
= ,
,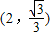 ;(7分)
;(7分)

科目:初中数学 来源:2010年广东省肇庆市高要市中考数学二模试卷(解析版) 题型:解答题
 上.
上. 与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
查看答案和解析>>
科目:初中数学 来源:2010年广东省肇庆市高要市中考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年广东省肇庆市高要市中考数学二模试卷(解析版) 题型:解答题
 的图象经过点(-1,3)
的图象经过点(-1,3)查看答案和解析>>
科目:初中数学 来源:2006年湖南省湘潭市中小学教师业务理论考试初中数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com