

| 边数 | 三 | 四 | 五 | 六 | 七 | … | n |
| 对角线条数 | 0 | 2 | 5 | … |
 ;
;| 边数 | 三 | 四 | 五 | 六 | 七 | … | n | ||
| 对角线条数 | 0 | 2 | 5 | 9 | 14 | … |
|
| 10×(10-3) |
| 2 |


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:

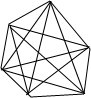
查看答案和解析>>
科目:初中数学 来源: 题型:
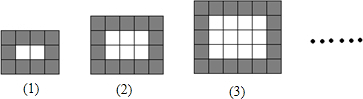
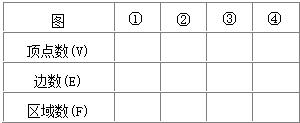
| 图形编号 | (1) | (2) | (3) | (4) | … |
| 黑色瓷砖的块数 | 10 | 14 | 18 | 22 22 |
… |
| 白色瓷砖的块数 | 2 | 6 | 12 | 20 20 |
… |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:解答题
按如图所示的规律用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,并解答下面问题: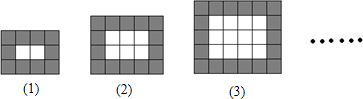
(1)将下表填写完整
| 图形编号 | (1) | (2) | (3) | (4) | … |
| 黑色瓷砖的块数 | 10 | 14 | 18 | ______ | … |
| 白色瓷砖的块数 | 2 | 6 | 12 | ______ | … |
(2)第(n)个图形中,共有黑色瓷砖______块,共有白色瓷砖______块;(用含n的代数式表示,答案直接写在题中横线上);
(3)如果每块黑色瓷砖12元每块白瓷砖10元,求购买铺设第(8)个图形所需瓷砖的费用;
(4)是否存在第(n)个图形,该图形所需白、黑瓷砖的总数为18325块?若存在,求出该图形的编号n;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com