
 在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,求△ABC的面积.
在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,求△ABC的面积. 分析 首先根据重心到顶点的距离与重心到对边中点的距离之比为2:1,判断出BO=2OE,进而求出S△DOE、S△BDE的大小;然后根据点D是BC的中点,判断出S△CDE=S△BDE,进而求出S△BCE的大小;最后根据点E是AC的中点,判断出S△ABE=S△BCE,进而求出S△ABC的大小即可.
解答 解:如图,连接DE,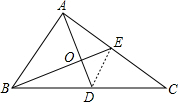 ,
,
∵中线AD、BE相交于点O,
∴点O是△ABC的重心,
∴BO=2OE,
∴S△DOE=$\frac{1}{2}$S△BOD=$\frac{1}{2}×5$=$\frac{5}{2}$,
∴S△BDE=5$+\frac{5}{2}=\frac{15}{2}$,
∵点D是BC的中点,
∴BD=DC,
∴S△CDE=S△BDE,
∴S△BCE=$\frac{15}{2}+\frac{15}{2}=15$,
∵点E是AC的中点,
∴AE=CE,
∴S△ABE=S△BCE,
∴S△ABC=15×2=30,
即△ABC的面积是30.
点评 (1)此题主要考查了三角形的重心的判断和性质的应用,要熟练掌握,解答此题的关键是要明确:重心到顶点的距离与重心到对边中点的距离之比为2:1.
(2)此题还考查了三角形的面积的求法,要熟练掌握,解答此题的关键是要明确:两个三角形的高一定时,它们面积的比等于它们底边的长度的比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<1 | B. | a≤1 | C. | a>1 | D. | a≥1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,从西到东的轻轨线经过A镇和B镇,两镇相距18千米,某公司C位于B镇的正南4千米处,现要从A镇把货物运往公司C,需要在轻轨线上的D处修筑通往公司C的公路.如果要使A镇到D处(沿轻轨)再到公司C处(沿公路)的总路程为20千米,那么D处距离A镇多少千米?
如图,从西到东的轻轨线经过A镇和B镇,两镇相距18千米,某公司C位于B镇的正南4千米处,现要从A镇把货物运往公司C,需要在轻轨线上的D处修筑通往公司C的公路.如果要使A镇到D处(沿轻轨)再到公司C处(沿公路)的总路程为20千米,那么D处距离A镇多少千米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
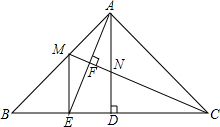 已知:如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.CM⊥AE,垂足是F,交AD于N,交AB于M,连接ME.
已知:如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.CM⊥AE,垂足是F,交AD于N,交AB于M,连接ME.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com