
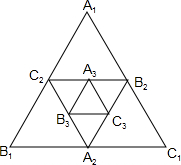
 如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=$\frac{\sqrt{3}}{{4}^{20}}$.
如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=$\frac{\sqrt{3}}{{4}^{20}}$. 分析 根据相似三角形的性质,先求出正△A2B2C2,正△A3B3C3的面积,依此类推△AnBnCn的面积是$\frac{\sqrt{3}}{4}$($\frac{1}{4}$)n-1,从而求出第20个正△A20B20C20的面积.
解答 解:正△A1B1C1的面积是$\frac{\sqrt{3}}{4}$,
而△A2B2C2与△A1B1C1相似,并且相似比是1:2,
则面积的比是$\frac{1}{4}$,则正△A2B2C2的面积是$\frac{\sqrt{3}}{4}$×$\frac{1}{4}$;
因而正△A3B3C3与正△A2B2C2的面积的比也是,面积是$\frac{\sqrt{3}}{4}$×($\frac{1}{4}$)2;
依此类推△AnBnCn与△An-1Bn-1Cn-1的面积的比是$\frac{1}{4}$,第n个三角形的面积是$\frac{\sqrt{3}}{4}$($\frac{1}{4}$)n-1.
所以第20个正△A20B20C20的面积是$\frac{\sqrt{3}}{{4}^{20}}$.
故答案为:$\frac{\sqrt{3}}{{4}^{20}}$.
点评 本题考查了相似三角形的性质及应用,相似三角形面积的比等于相似比的平方,找出规律是关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:选择题
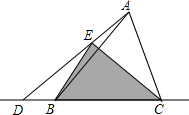 如图,D是给定△ABC边BC所在直线上一动点,E是线段AD上一点,DE=2AE,连接BE,CE,点D从B的左边开始沿着BC方向运动,则△BCE的面积变换情况是( )
如图,D是给定△ABC边BC所在直线上一动点,E是线段AD上一点,DE=2AE,连接BE,CE,点D从B的左边开始沿着BC方向运动,则△BCE的面积变换情况是( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 先变小后变大 | D. | 始终不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若斜坡AF的坡度i=1:$\sqrt{3}$,则大树的高度为( )(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.732)
如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若斜坡AF的坡度i=1:$\sqrt{3}$,则大树的高度为( )(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.732)| A. | 11米 | B. | 12米 | C. | 13米 | D. | 14米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
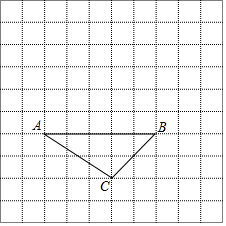 如图,已知△ABC.
如图,已知△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com