
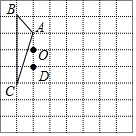
 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:分析 (1)利用网格特点和旋转的性质画出点A、B、C的对应点A′、B′、C′即可;
(2)利用弧长公式求解;
(3)把BC分为两段BC′、CC′,然后利用扇形的面积之差分别计算BC′、CC′所扫过的面积;
(4)延长AO到A″使OA″=2OA,则点A″为点A的对应点,同样方法作出B、C的对应点B″、C″,从而得到△A″B″C″.
解答 解:(1)如图,△A′B′C′为所作;
(2)DC=$\sqrt{2}$,
所以点C所经过的路径长=$\frac{90•π•\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π;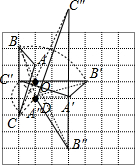
(3)DB=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
所以线段BC旋转过程中扫过的面积=2[$\frac{90•π•(\sqrt{2})^{2}}{360}$-$\frac{90•π•{1}^{2}}{360}$]+[$\frac{90•π•(\sqrt{10})^{2}}{360}$-$\frac{90•π•(\sqrt{2})^{2}}{360}$]=$\frac{5}{2}$π;
(4)如图,△A″B″C″为所作.
点评 本题考查了作图-位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了轴对称变换和旋转变换.


科目:初中数学 来源: 题型:解答题
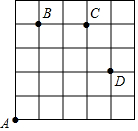 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
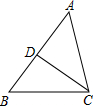 如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2
如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
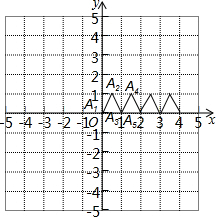 一只电子青蛙在如图的平面直角坐标系做如下运动:从坐标原点开始起跳记为A1,然后沿着边长为1的等边三角形跳跃即A1→A2→A3→A4→A5…已知A3的坐标为(1,0),则A2014的坐标是(1006,$\frac{\sqrt{3}}{2}$).
一只电子青蛙在如图的平面直角坐标系做如下运动:从坐标原点开始起跳记为A1,然后沿着边长为1的等边三角形跳跃即A1→A2→A3→A4→A5…已知A3的坐标为(1,0),则A2014的坐标是(1006,$\frac{\sqrt{3}}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com