练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．把抛物线y=x2沿直线y=x向上平移2$\sqrt{2}$个单位后，则平移后的抛物线解析式是y=x2-4x+6．

    分析 沿直线y=x向上平移2$\sqrt{2}$个单位，即向右平移2个单位长度，向上平移2个单位长度，利用平移法则即可求解．

    解答 解：沿直线y=x向上平移2$\sqrt{2}$个单位，即向右平移2个单位长度，向上平移2个单位长度．
    则抛物线y=x2沿y=x向上平移2$\sqrt{2}$个单位后抛物线解析式是y=（x-2）2+2．即y=x2-4x+6．
    故答案是：y=x2-4x+6．

    点评 此题考查了二次函数图象的平移与几何变换，利用抛物线解析式的变化规律：左加右减，上加下减是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．当a=$\sqrt{2}$，b=1时，代数式（a+2b）（a-2b）的值为（　　）
    A．3B．0C．-1D．-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：先化简，再求值：
    （1）计算：-22+$\sqrt{8}$cos45°+（-$\frac{1}{2}$）-2-（π-2017）0
    （2）先化简：$\frac{{x}^{2}+x}{{x}^{2}+2x+1}$÷（$\frac{2}{x+1}$-$\frac{1}{x}$），然后再从-2≤x＜2的范围内选取一个合适的x的整数值代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．将两张长方形纸片如图所示摆放，使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上，则∠1和∠2的关系是（　　）
    A．∠1=∠2B．∠1+∠2=90°C．∠1+∠2=180°D．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．已知抛物线y=ax2+bx+c（a＜b＜0）与x轴最多有一个交点，现有以下结论：
    ①c＜0；②该抛物线的对称轴在y轴左侧；③关于x的方程ax2+bx+c+2=0有实数根；④对于自变量x的任意一个取值，都有$\frac{a}{b}$x2+x≥-$\frac{b}{4a}$，其中正确的为（　　）
    A．①②B．①②④C．①②③D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

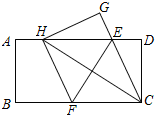    16．如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点H处，点D落在点G处，有以下四个结论：
    ①四边形CFHE是菱形；②线段BF的取值范围为3≤BF≤4；
    ③EC平分∠DCH；④当点H与点A重合时，EF=2$\sqrt{5}$
    以上结论中，你认为正确的有①②④．（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．把多项式3ax2+6a2x+3a3分解因式的结果是3a（x+a）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．随着某市养老机构建设稳步推进，拥有的养老床位不断增加，养老床位数从2014年底的2万个增长到2016年底的2.88万个，则该市这两年拥有的养老床位数的平均年增长率为20%．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

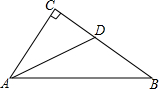    1．如图，在△ABC中，∠C=90°，∠CAB的平分线交BC于点D，若AB=5，AC=3，则△DAB的面积为（　　）
    A．3B．$\frac{15}{4}$C．5D．$\frac{25}{8}$

    查看答案和解析>>

    同步练习册答案