
【题目】如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,求⊙O的半径.
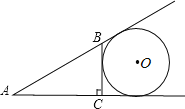
【答案】2
【解析】试题分析:分析:先连接OD、OE根据⊙O与△ABC中AB、AC的延长线及BC边相切,得出AF=AD,BE=BF,CE=CD,再根据OD⊥AD,OE⊥BC,∠ACB=90°,得出四边形ODCE是正方形,最后设OD=r,列出5+3-r=4+r,求出r=2即可.
试题解析:
连接OD、OE,
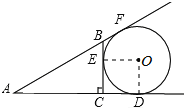
∵⊙O与△ABC中AB、AC的延长线及BC边相切,
∴AF=AD,BE=BF,CE=CD,
OD⊥AD,OE⊥BC,
∵∠ACB=90°,
∴四边形ODCE是正方形,
设OD=r,则CD=CE=r,
∵BC=3,
∴BE=BF=3-r,
∵AB=5,AC=4,
∴AF=AB+BF=5+3-r,
AD=AC+CD=4+r,
∴5+3-r=4+r,
r=2,
则⊙O的半径是2.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,DE是△ABC的中位线,AF是△ABC的中线.
求证DE=AF.

证法1:∵DE是△ABC的中位线,
∴DE= .
∵AF是△ABC的中线,∠BAC=90°,
∴AF= ,
∴DE=AF.
请把证法1补充完整,并用不同的方法完成证法2.
证法2:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-5)-(+3)+(-9)-(-7); (2)-|-2|-(-3)2÷(-1)2;
(3)![]() ; (4)-14-(1-0.5)÷
; (4)-14-(1-0.5)÷![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
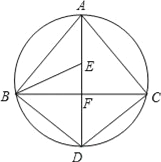
【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
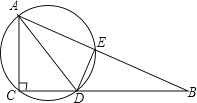
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)若AC=6,CB=8,求△ACD外接圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动了3个单位长度,再向左移动 5 个单位长度,可以看到终点表示的数是![]() .已知点
.已知点![]() 、
、![]() 是数轴上的点,完成下列各题:
是数轴上的点,完成下列各题:
![]()
(1)如果点![]() 表示数- 3,将点
表示数- 3,将点![]() 向右移动 7 个单位长度,那么终点
向右移动 7 个单位长度,那么终点![]() 表示的数是 ,
表示的数是 ,![]() 、
、![]() 两点间的距离是 .
两点间的距离是 .
(2)如果点![]() 表示数是3,将点
表示数是3,将点![]() 向左移动 7 个单位长度,再向右移动5 个单位长度,那么终点
向左移动 7 个单位长度,再向右移动5 个单位长度,那么终点![]() 表示的数是 ,
表示的数是 ,![]() 、
、 ![]() 两点间的距离是 .
两点间的距离是 .
(3)一般地,如果点![]() 表示数为
表示数为![]() ,将点
,将点![]() 向右移动
向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,那么请你猜想终点
个单位长度,那么请你猜想终点![]() 表示的数是 ,
表示的数是 ,![]() 、
、![]() 两点间的距离是 .
两点间的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号中:8,﹣![]() ,+2.8,π,
,+2.8,π,![]() ,﹣0.003,0,﹣100,﹣3.626626662……
,﹣0.003,0,﹣100,﹣3.626626662……
正数集合{_____ …}
整数集合{_____…}
负分数集合{_____ …}
无理数集合{_____ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4正方形的网格中,线段AB,CD如图位置,每个小正方形的边长都是1.
(1)求出线段AB、CD的长度;
(2)在图中画出线段EF,使得EF=![]() ,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
(3)我们把(2)中三条线段按照点E与点C重合,点F与点B重合,点D与点A重合,这样可以得△ABC,则点C到直线AB的距离为______(直接写结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(﹣1,y1),(2,y2),![]() 在反比例函数y=﹣
在反比例函数y=﹣![]() 的图象上,则下列关系式正确的是( )
的图象上,则下列关系式正确的是( )
A.y3<y2<y1B.y2<y3<y1
C.y3<y1<y2D.y2<y1<y3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com