
| 周数x | 1 | 2 | 3 | 4 |
| 价格y1(元/桶) | 60 | 59 | 58 | 57 |
分析 (1)根据表格数据,可得出y1与x的函数关系式;将点(1,54),(2,57)代入,可得出y2与x的函数关系式;
(2)分别得出二月份、三月份的利润表达式,然后利用配方法求出最值,继而比较可得出答案.
(3)根据题意,令x=2求出m2,令x=3求出y2,然后列出方程,解出a的值即可,注意考虑实际情况进行取舍.
解答 解:(1)9月份:根据表格可得:y1=-x+61(1≤x≤4,x为整数);
10月份:∵当x=1时,y=54;当x=2时,y=57,
∴$\left\{\begin{array}{l}{b+c-\frac{1}{4}=54}\\{2b+c-1=57}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=\frac{15}{4}}\\{c=\frac{101}{2}}\end{array}\right.$
故y2=-$\frac{1}{4}$x2+$\frac{15}{4}$x+$\frac{101}{2}$.
(2)设第x周的利润为w元,
9月份:w=y1-m1=(-x+61)-($\frac{1}{3}$x2-3x+50)=-$\frac{1}{3}$x2+2x+11=-$\frac{1}{3}$(x-3)2+14,
∵-$\frac{1}{3}$<0,
∴开口向下,
又∵对称轴是:直线x=3,
∴当x=3时,w最大=14;
10月份:w=y2-m2=-$\frac{1}{4}$x2+$\frac{15}{4}$x+$\frac{101}{2}$-($\frac{7}{2}$x+$\frac{81}{2}$)=-$\frac{1}{4}$x2+$\frac{1}{4}$x=10=-$\frac{1}{4}$(x-$\frac{1}{2}$)2+$\frac{161}{16}$
∵-$\frac{1}{4}$<0,
∴开口向下,
又∵对称轴是:直线x=$\frac{1}{2}$,
∴当1≤x≤4时,w随x的增大而减小,
∴当x=1时,w最大=10,
∵14>10,
∴9月份的第3周,利润最大,最大利润为14元/桶.
(3)在m2=$\frac{7}{2}$x+$\frac{81}{2}$中,令x=2,得:m2=$\frac{95}{2}$,
在y2=-$\frac{1}{4}$x2+$\frac{15}{4}$x+$\frac{101}{2}$中,令x=3,得:y2=$\frac{119}{2}$,
∴a%×1200×($\frac{119}{2}-\frac{95}{2}$)+(1-a%)×1200×($\frac{119}{2}-\frac{95}{2}$-4)=12000,
解得:a=50.
点评 本题考查了二次函数的应用,题目所给信息量比较大,注意仔细审题,得到解题需要的信息,将实际问题转化为数学模型进行求解,难度较大.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$=$\frac{{a}^{2}}{{b}^{2}}$ | B. | $\frac{a}{b}$=$\frac{a+c}{b+c}$ | C. | $\frac{a}{b}$=$\frac{a-c}{b-c}$ | D. | $\frac{a}{b}$=$\frac{ma}{mb}$(m≠0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
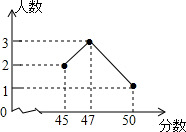 在2015年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数分别是( )
在2015年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数分别是( )| A. | 3,2.5 | B. | 47,46 | C. | 47,47 | D. | 50,47 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
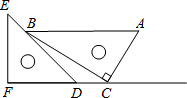 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=2,则CD的长为3-$\sqrt{3}$.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=2,则CD的长为3-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
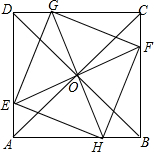 已知;如图,在正方形ABCD中,AC与BD相交于点O,EF,GH都过点O,分别交AD,BC于E,F,交CD,AB于G,H,EF⊥GH,求证:四边形EHFG是正方形.
已知;如图,在正方形ABCD中,AC与BD相交于点O,EF,GH都过点O,分别交AD,BC于E,F,交CD,AB于G,H,EF⊥GH,求证:四边形EHFG是正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com