
【题目】如图,已知四边形![]() 是矩形,点
是矩形,点![]() 在对角线
在对角线![]() 上,点
上,点![]() 在边
在边![]() 上(点
上(点![]() 与点
与点![]() 、
、![]() 不重合),
不重合),![]() ,且
,且![]() .
.
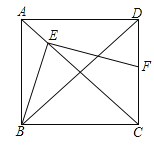
(1)求证:四边形![]() 是正方形;
是正方形;
(2)联结![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
【答案】(1)四边形![]() 是正方形(过程见详解)
是正方形(过程见详解)
(2)![]() (过程见详解)
(过程见详解)
【解析】
(1)本题借助辅助线利用![]() ,
,![]() ,找出∠DAC=45°得到DA=DC,即可证明,
,找出∠DAC=45°得到DA=DC,即可证明,
(2)本题在(1)的条件下证明△CBE![]() △DFQ,即可求证.
△DFQ,即可求证.
(1)

分别作EP⊥BC,EM⊥CD,
∵四边形ABCD为矩形,
∴∠ABE=∠BEP,
又BE⊥EF,
∴∠BEP+∠FEP=∠FEP+∠FEM=90°,
∴∠BEP =∠FEM,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即∠CEM=45°,
∴∠DAC=45°,
∴DA=DC,
∴矩形ABCD为正方形.
(2)
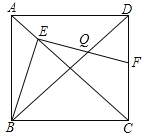
由(1)得:∠QDF=∠BCE=45°,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即∠EBC=∠DFQ(三角形外角等于与其不相邻两内角和),
∴△CBE![]() △DFQ,
△DFQ,
∴![]() ,
,
∴DF![]() EC=DQ
EC=DQ![]() BC,
BC,
即![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】学校为表彰在“了不起我的国”演讲比赛中获奖的选手,决定购买甲、乙两种图书作为奖品.已知购买30本甲种图书,50本乙种图书共需1350元;购买50本甲种图书,30本乙种图书共需1450元.
(1)求甲、乙两种图书的单价分别是多少元?
(2)学校要求购买甲、乙两种图书共40本,且甲种图书的数量不少于乙种图书数量的![]() ,请设计最省钱的购书方案.
,请设计最省钱的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2![]() 米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).
米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).
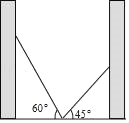
查看答案和解析>>
科目:初中数学 来源: 题型:
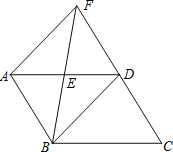
【题目】如图,ABCD中,E为AD的中点,直线BE、CD相交于点F.连接AF、BD.
(1)求证:AB=DF;
(2)若AB=BD,求证:四边形ABDF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019新型冠状病毒,因武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名“2019-nCoV”.冠状病毒是一个大型病毒家族,借助电子显微镜,我们可以看到这些病毒直径约为125纳米(1纳米=1 ![]() 10-9米),125纳米用科学记数法表示等于( )米
10-9米),125纳米用科学记数法表示等于( )米
A.1.25![]() 10-10B.1.25
10-10B.1.25![]() 10-11C.1.25
10-11C.1.25 ![]() 10-8D.1.25
10-8D.1.25![]() 10-7
10-7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装专卖店计划购进A,B两种型号的精品女装.已知3件A型女装和2件B型女装共需5400元;2件A型女装和1件B型女装共需3200元.
(1)求A,B两种型号女装的单价;
(2)专卖店购进A,B两种型号的女装共60件,其中A型的件数不少于B型件数的2倍,如果B型打八折,那么该专卖店至少需要准备多少货款.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com