
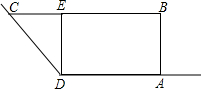
 某农场拟建一个梯形饲养场ABCD,其中AD,CD分别靠现有墙DM,DN,其余用新墙砌成,墙DM长为9米,墙DN足够长,两面墙形成的角度为135°,新墙DE将饲养场隔成△CDE和矩形ABED两部分.已知新建墙体总长为30米.设AB=x米,梯形饲养场ABCD的面积为S米2.
某农场拟建一个梯形饲养场ABCD,其中AD,CD分别靠现有墙DM,DN,其余用新墙砌成,墙DM长为9米,墙DN足够长,两面墙形成的角度为135°,新墙DE将饲养场隔成△CDE和矩形ABED两部分.已知新建墙体总长为30米.设AB=x米,梯形饲养场ABCD的面积为S米2.分析 (1)根据矩形和等腰直角三角形的性质得出AB=DE=CE=x米,AD=BE=30-3x米,再由矩形和三角形的面积公式可得S关于x的函数解析式;
(2)由墙DM长为9米得出x的取值范围,再将函数解析式配方成顶点式,根据二次函数的性质可得最值情况.
解答 解:(1)∵四边形ABED是矩形,
∴AB=CE=x米,∠ADE=∠DEC=90°,
∵∠ADC=135°,
∴∠EDC=∠DCE=45°,
∴CE=DE=x米,
∴BE=30-3x米,
∴S=x(30-3x)+$\frac{1}{2}$x2=-$\frac{5}{2}$x2+30x;
(2)∵30-3x≤9,
∴x≥7,
S=-$\frac{5}{2}$x2+30x=-$\frac{5}{2}$(x-6)2+90,
∵当x>6时,S随x的增大而减小,
∴当x=7时,Smax=87.5,
答:当x=7时,饲料场ABCD的面积最大,最大面积为87.5平方米.
点评 本题主要考查二次函数的应用,熟练掌握矩形和等腰直角三角形的性质得出函数解析式和二次函数的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a-b|.
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a-b|.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
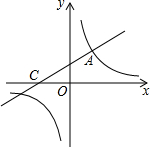 直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(2,3).
直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -1 | 0 | 2 | 3 | 4 | … |
| y | … | 5 | 2 | 2 | 5 | 10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
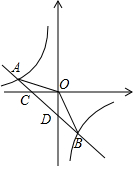 如图,在平面直角坐标系中,一次函数y=ax-1(a≠0)的图象与x轴交于点C,与y轴交于点D,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,点B的坐标是(3,m),连接OB,tan∠BOD=$\frac{3}{4}$.
如图,在平面直角坐标系中,一次函数y=ax-1(a≠0)的图象与x轴交于点C,与y轴交于点D,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,点B的坐标是(3,m),连接OB,tan∠BOD=$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com