
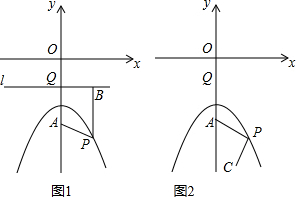
���� ��1�������A��P��B�����꼴����ã������A��P��B�����꼴����ã�
��2�����ö��κ���ͼ���ϵ��������������P��m��-$\frac{1}{4}$m2-2������B��m��-1����Ȼ����������ľ��빫ʽ�����PA��PB���Ӷ����ж�������ȣ�
��3������Q��QB��x�ᣬ��P����PB��QB��B�㣬��ͼ2����PB=PA����������֮���߶���̣�����P��B��C����ʱ����ʱP��ĺ�����Ϊ2��Ȼ������Ӧ�ĺ���ֵ���ɵõ�P�����꣮
��� �⣺��1���ٵ�m=0ʱ����P��0��n����
����y=-$\frac{1}{4}$x2-2�ã�n=-2��
��P��0��-2����
��B����Q���غϣ�
�ߵ�A��0��-3������Q��0��-1����
��PA=1��PB=1��
�ڵ�m=2ʱ����P��2��n����
����y=-$\frac{1}{4}$x2-2�ã�n=-3��
��P��2��-3����
�ߵ�A��0��-3������Q��0��-1����
��PA=$\sqrt{{2}^{2}+{0}^{2}}$=2��PB=2��
�ʴ�Ϊ��1��1��2��2��
��2������PA��PB��ȣ�
�������£���P��m��-$\frac{1}{4}$m2-2������B��m��-1����
��PA=$\sqrt{{m}^{2}+��-\frac{1}{4}m-2+3��^{2}}$=$\sqrt{��\frac{1}{4}{m}^{2}+1��^{2}}$=$\frac{1}{4}$m2+1��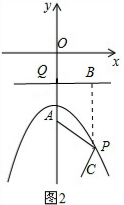
PB=-1-��-$\frac{1}{4}$m2-2��=$\frac{1}{4}$m2+1��
��PA=PB��
��3�����ڣ�
����Q��QB��x�ᣬ��P����PB��QB��B�㣬��ͼ2��
��PB=PA��
��PA+PC=PB+PC��
����P��B��C����ʱ��PB+PC��С����ʱPC��QB��P��ĺ�����Ϊ2��
��x=2ʱ��y=-$\frac{1}{4}$x2-2=-$\frac{1}{4}$��4-2=-3��
����ʱP������Ϊ��2��-3����
���� �����Ƕ��κ������ۺ��⣬�����˶��κ���ͼ���ϵ�������������ô���ϵ������һ�κ�������ʽ������������ͼ�����ʣ���ס�����ľ��빫ʽ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC��DΪBC���е㣬DE��AB�ڵ�E��DF��AC�ڵ�F����DEF��ʲô�����Σ�˵�����ɣ�
��ͼ���ڡ�ABC�У�AB=AC��DΪBC���е㣬DE��AB�ڵ�E��DF��AC�ڵ�F����DEF��ʲô�����Σ�˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com