【题目】如图，AB交CD于O，OE⊥AB．
（1）若∠EOD=20°，求∠AOC的度数；
（2）若∠AOC：∠BOC=1：2，求∠EOD的度数．
【答案】(1)、70°；(2)、30°
【解析】试题分析：(1)、首先根据垂直得出∠AOE=90°，根据∠AOC=180°－∠AOE－∠EOD得出答案；(2)、首先设∠AOC=x，则∠BOC=2x，根据平角的性质得出x的值，根据∠EOD=180°－AOE－∠AOC得出答案.
试题解析：(1)、∵OE⊥AB， ∴∠AOE=90°， ∵∠EOD=20°， ∴∠AOC=180°﹣90°﹣20°=70°；
(2)、设∠AOC=x，则∠BOC=2x， ∵∠AOC+∠BOC=180°， ∴x+2x=180°， 解得：x=60°，
∴∠AOC=60°， ∴∠EOD=180°﹣90°﹣60°=30°．
科目：初中数学 来源： 题型：
【题目】已知，点M是二次函数y=ax2（a＞0）图象上的一点，点F的坐标为（0，
），直角坐标系中的坐标原点O与点M，F在同一个圆上，圆心Q的纵坐标为
．
（1）求a的值；
（2）当O，Q，M三点在同一条直线上时，求点M和点Q的坐标；
（3）当点M在第一象限时，过点M作MN⊥x轴，垂足为点N，求证：MF=MN+OF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y=a（x﹣6）2+h．已知球网与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m．
（1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）
（2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；
（3）若球一定能越过球网，又不出边界，求h的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
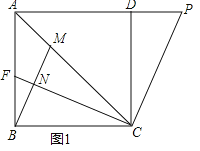
【题目】如图1，在正方形ABCD中，点P为AD延长线上一点，连接AC、CP，过点C作CF⊥CP交于C，交AB于点F，过点B作BM⊥CF于点N，交AC于点M．
（1）若AP=
AC，BC=4，求S△ACP；
（2）若CP﹣BM=2FN，求证：BC=MC；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某宾馆有50个房间供游客居住，当每个房间定价120元时，房间会全部住满，当每个房间每天的定价每增加10元时，就会有一个房间空闲。如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，设每个房间定价增加10 x元（x为整数）。
⑴（2分）直接写出每天游客居住的房间数量y与x的函数关系式。
⑵（4分）设宾馆每天的利润为W元，当每间房价定价为多少元时，宾馆每天所获利润最大，最大利润是多少？
⑶（4分）某日，宾馆了解当天的住宿的情况，得到以下信息：①当日所获利润不低于5000元，②宾馆为游客居住的房间共支出费用没有超过600元，③每个房间刚好住满2人。问：这天宾馆入住的游客人数最少有多少人？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
