
【题目】2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
频率分布表
分数段 | 频数 | 频率 |
50.5~60.5 | 16 | 0.08 |
60.5~70.5 | 40 | 0.2 |
70.5~80.5 | 50 | 0.25 |
80.5~90.5 | m | 0.5 |
90.5~100.5 | 24 | n |

(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n ;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
科目:初中数学 来源: 题型:
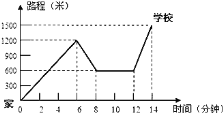
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校,以下是他本次上学所用的时间与路程的关系示意图,根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是______米;
(2)小明在书店停留了______分钟;
(3)本次上学途中,小明一共行驶了_____米,一共用了_______分钟;
(4)在整个上学的途中________(哪个时间段)小明骑车速度最快,最快的速度是____米/分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为![]() ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
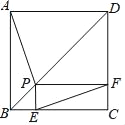
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC,AC上,抛物线P上的部分点的横坐标对应的纵坐标如下.

(1)求A,B,C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并指出m的取值范围;
(3)当矩形DEFG的面积S最大时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围;
(4)若点D的坐标为(1,0),求矩形DEFG的面积.
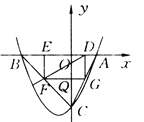
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里(将各数用逗号分开):
+8,0.275,-|-2|,0,-1.04,-(-10),![]() ,
,![]() ,
,![]() ,0.1.
,0.1.
正整数:﹛ …﹜
整数:﹛ …﹜
负有理数: ﹛ …﹜
分数: ﹛ …﹜
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元初,中美洲马雅人使用的一种数字系统与其他计数方式都不相同,它采用二十进位制但只有3个符号,用点“![]() ”、划“—”、卵形“
”、划“—”、卵形“![]() ”来表示我们所使用的自然数,如自然数1-19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1-19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
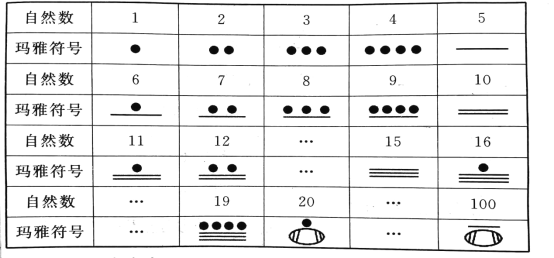
(1)玛雅符号![]() 表示的自然数是哪个数;
表示的自然数是哪个数;
(2)请你画出表示自然数280的玛雅符号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
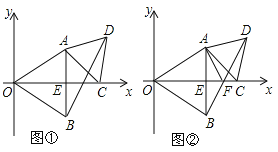
【题目】如图,△AOB和△ACD是等边三角形,其中AB⊥x轴于E点,点E坐标为(3,0),点C(5,0).
(1)如图①,求BD的长;
(2)如图②,设BD交x轴于F点,求证:∠OFA=∠DFA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com