
| x/人次 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 |
| y/元 | -3000 | -2000 | -1000 | 0 | 1000 | 2000 |
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{{({-2})}^2}}=-2$ | B. | $\sqrt{{{({-3})}^2}}=9$ | C. | $\sqrt{x^2}=x$ | D. | $\sqrt{{{({-5})}^2}}=5$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
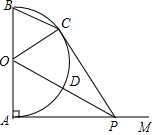 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AB=DC,下列所给的条件不能证明△ABC≌△DCB的是( )
如图,已知AB=DC,下列所给的条件不能证明△ABC≌△DCB的是( )| A. | ∠A=∠D=90° | B. | ∠ABC=∠DCB | C. | ∠ACB=∠DBC | D. | AC=BD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com