
【题目】在菱形ABCD中,∠ABC=60°
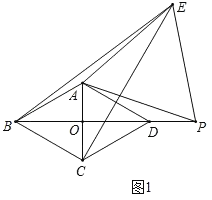
(1)如图1,P是边BD延长线上一点,以AP为边向右作等边△APE,连接BE、CE.
①求证:CE⊥AD;
②若AB=![]() ,BE=
,BE=![]() ,求AE的长;
,求AE的长;
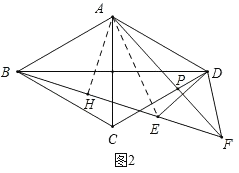
(2)如图2,P是边CD上一点,点D关于AP的对称点为E,连接BE并延长交AP的延长线于点F,连接DE、DF.若BE=11,DE=5,求△ADF的面积.

【答案】(1)①证明见解析;②AE=![]() ;(2)△ADF的面积为
;(2)△ADF的面积为![]() .
.
【解析】
(1)①证△ADC和△ABC是等边三角形,再证△BAP≌△CAE,推出∠ACE=30°,由∠ACE+∠CAD=90°即可证明结论;
②如图1,设AC与BD交于点O,证∠BCE=90°,由勾股定理求出CE,BP的长,由锐角三角函数等分别求出OA,OP的长,由勾股定理即可求出AP的长,即AE的长;
(2)如图2,连接AE,过点A作AH⊥BF于点H,证∠HAF=![]() ∠BAD=60°,再证△DEF为等边三角形,即可求出HF,AH的长,进一步求出△AEF的面积,证△ADF≌△AEF即可.
∠BAD=60°,再证△DEF为等边三角形,即可求出HF,AH的长,进一步求出△AEF的面积,证△ADF≌△AEF即可.
证明: (1)①在菱形ABCD中,∠ABC=60°,
∴∠ADC=60°,且AB=BC=DA=DC,
∴△ADC和△ABC是等边三角形,
∴AB=AC,∠BAC=∠CAD=60°,
又∵△APE是等边三角形,
∴AE=AP,∠EAP=60°,
∴∠BAC+∠CAP=∠PAE+∠CAP,
即∠BAP=∠CAE,
∴△BAP≌△CAE(SAS),
∴∠ACE=∠ABP=![]() ∠ABC=30°,
∠ABC=30°,
∵∠CAD=60°,
∴∠ACE+∠CAD=90°,
∴CE⊥AD;
②解:如图1,设AC与BD交于点O,
由①知,∠ACE=30°,且∠ACB=60°,
∴∠ACE+∠ACB=∠BCE=90°,
∵在Rt△BCE中,BC=AB=![]() ,BE=
,BE=![]() ,
,
∴CE=![]() =4,
=4,
由①知,△BAP≌△CAE,
∴BP=CE=4,
在Rt△BOC中,∠ACB=60°,
∴BO=![]() BC=
BC=![]() ,CO=AO=
,CO=AO=![]() BC=
BC=![]() ,
,
∴OP=BP﹣BO=![]() ,
,
∴在Rt△AOP中,
AP=![]() =
=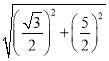 =
=![]() ,
,
∴AE=AP=![]() ;
;
(2)解:如图2,连接AE,过点A作AH⊥BF于点H,
∵点D关于AP的对称点为E,
∴AP垂直平分DE,
∴AD=AE,FD=FE,
∴∠EAF=∠DAF=![]() ∠EAD,∠DFA=∠EFA=
∠EAD,∠DFA=∠EFA=![]() ∠DFE,
∠DFE,
又∵在菱形ABCD中,AB=AD,
∴AB=AE,
∴AH垂直平分BE,
∴EH=BH=![]() BE=
BE=![]() ,∠BAH=∠EAH=
,∠BAH=∠EAH=![]() ∠BAE,
∠BAE,
∴∠HAF=∠EAH+∠EAF=![]() ∠BAD,
∠BAD,
∵∠ABC=60°,
∴∠BAD=180°﹣∠ABC=120°,
∴∠HAF=60°,
∴∠AFH=90°﹣∠HAF=30°,
∴∠DFE=60°,
∴△DEF为等边三角形,
∴EF=DE=5,
∴HF=HE+EF=![]() +5=
+5=![]() ,
,
在Rt△AHF中,∠AFH=30°,
∴AH=![]() HF=
HF=![]() ,
,
∴S△AEF=![]() EFAH=
EFAH=![]() ×5×
×5×![]() =
=![]() ,
,
∵AD=AE,FD=FE,AF=AF,
∴△ADF≌△AEF(SSS),
∴△ADF的面积为![]() .
.


科目:初中数学 来源: 题型:
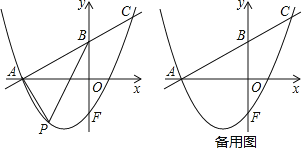
【题目】如图,已知在平面直角坐标系xOy中,直线y=![]() x+
x+![]() 与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=
与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=![]() x2+bx+c经过点A和点F,与直线AB交于点C.
x2+bx+c经过点A和点F,与直线AB交于点C.
(1)求b和c的值;
(2)点P是直线AC下方的抛物线上的一动点,连结PA,PB.求△PAB的最大面积及点P到直线AC的最大距离;
(3)点Q是抛物线上一点,点D在坐标轴上,在(2)的条件下,是否存在以A,P,D,Q为顶点且AP为边的平行四边形,若存在,直接写出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:①b2﹣4ac=0 ②a+b+c>0 ③2a﹣b=0④c﹣a=3,其中正确的有_____.(填序号)
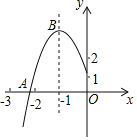
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
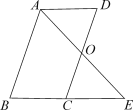
(1)求证:△AOD≌△EOC;
(2)连接AC、DE,当∠B=∠AEB=45°时,求证四边形 ACED是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球,放回、搅匀,下表是活动进行中的一组统计数据,
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.230 | 0.231 | 0.300 | 0.260 | 0.254 |
袋中白球的个数约为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
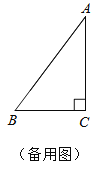
【题目】如图,在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.动点P,Q从点A同时出发,点P沿AB向终点B运动;点Q沿AC→CB向终点B运动,速度都是1cm/s.当一个点到达终点时,另一个点同时停止运动.设点P运动的时间为t(s),在运动过程中,点P,点Q经过的路线与线段PQ围成的图形面积为S(cm2).
(1)AC=_________cm;
(2)当点P到达终点时,BQ=_______cm;
(3)①当t=5时,s=_________;
②当t=9时,s=_________;
(4)求S与t之间的函数解析式.
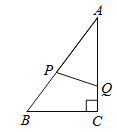
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC
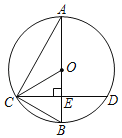
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是( )

A.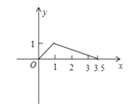 B.
B.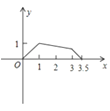 C.
C.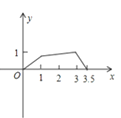 D.
D.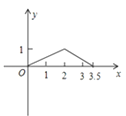
查看答案和解析>>
科目:初中数学 来源: 题型:
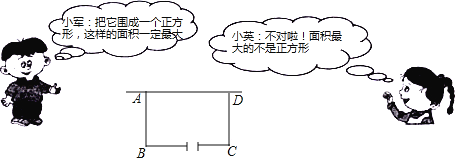
【题目】(9分)某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com