
| A. | m≤2或m≥3 | B. | m≤3或m≥4 | C. | 2<m<3 | D. | 3<m<4 |
分析 把A(4,4)代入抛物线y=ax2+bx+3得4a+b=$\frac{1}{4}$,根据对称轴x=-$\frac{b}{2a}$,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,所以$0<|2-(-\frac{b}{2a})|≤1$,解得$a≥\frac{1}{8}$或a$≤-\frac{1}{8}$,把B(2,m)代入y=ax2+bx+3得:4a+2b+3=m,得到a=$\frac{7}{8}-\frac{m}{4}$,所以$\frac{7}{8}-\frac{m}{4}≥\frac{1}{8}$或$\frac{7}{8}-\frac{m}{4}≤-\frac{1}{8}$,即可解答.
解答 解:把A(4,4)代入抛物线y=ax2+bx+3得:
16a+4b+3=4,
∴16a+4b=1,
∴4a+b=$\frac{1}{4}$,
∵对称轴x=-$\frac{b}{2a}$,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,
∴$0<|2-(-\frac{b}{2a})|≤1$
∴$0<|\frac{4a+b}{2a}|≤1$,
∴|$\frac{1}{8a}$|≤1,
∴$a≥\frac{1}{8}$或a$≤-\frac{1}{8}$,
把B(2,m)代入y=ax2+bx+3得:
4a+2b+3=m
2(2a+b)+3=m
2(2a+$\frac{1}{4}$-4a)+3=m
$\frac{7}{2}$-4a=m,
a=$\frac{7}{8}-\frac{m}{4}$,
∴$\frac{7}{8}-\frac{m}{4}≥\frac{1}{8}$或$\frac{7}{8}-\frac{m}{4}≤-\frac{1}{8}$,
∴m≤3或m≥4.
故选:B.
点评 本题考查了二次函数的性质,解决本题的关键是根据点B到抛物线对称轴的距离记为d,满足0<d≤1,得到$0<|2-(-\frac{b}{2a})|≤1$.


科目:初中数学 来源: 题型:选择题
| A. | 1333 | B. | 1999 | C. | 2001 | D. | 2249 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
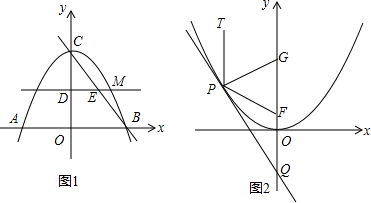
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
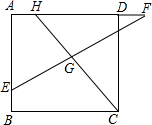 对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.
对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
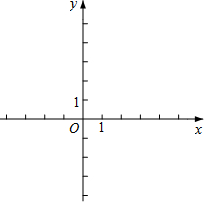 在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(-$\frac{1}{3}$,-$\frac{1}{3}$),(-$\sqrt{2}$,-$\sqrt{2}$),…,都是和谐点.
在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(-$\frac{1}{3}$,-$\frac{1}{3}$),(-$\sqrt{2}$,-$\sqrt{2}$),…,都是和谐点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{6-2x}{-x+3}$=2 | B. | $\frac{a-b}{(a-b)(a+b)}$=0 | C. | $\frac{(a-b)^{3}}{(b-a)^{3}}$=1 | D. | $\frac{(a-b)^{2}}{(b-a)^{2}}$=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com