
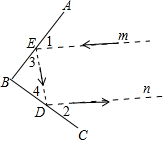
 如图,平面镜AB、BC相交于点B,一束光线m射到平面镜AB、BC上,经过在E、D两点反射出去,此时有∠1=∠3,∠2=∠4
如图,平面镜AB、BC相交于点B,一束光线m射到平面镜AB、BC上,经过在E、D两点反射出去,此时有∠1=∠3,∠2=∠4分析 (1)根据平角的定义求得∠5=80°,再根据光线m∥n,即可得出∠6=100°,再根据平角定义得出∠2=∠4=40°;
(2)先根据∠B=90°,得出∠3+∠4=90°,再根据∠1=∠3,∠2=∠4,求得∠1+∠2=90°,进而得出∠5+∠6=180°×2-90°×2=180°,即可判定光线m∥n.
解答 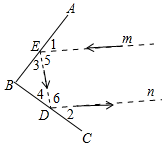 解:(1)∵∠3=∠1=50°,
解:(1)∵∠3=∠1=50°,
∴∠5=80°,
∵光线m∥n,
∴∠6=100°,
∴∠2=∠4=40°;
(2)当∠B=90°时,光线m∥n.
理由:∵∠B=90°,
∴∠3+∠4=90°,
又∵∠1=∠3,∠2=∠4,
∴∠1+∠2=90°,
∴∠5+∠6=180°×2-90°×2=180°,
∴光线m∥n.
点评 本题主要考查了平行线的性质与判定,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.


科目:初中数学 来源: 题型:填空题
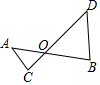 如图,已知直线AB与CD相交于点O,且∠DOB=∠ODB,若∠ODB=50°,则∠AOC的度数为50°;∠CAO是(填“是”或“不是”)∠AOC的同旁内角.
如图,已知直线AB与CD相交于点O,且∠DOB=∠ODB,若∠ODB=50°,则∠AOC的度数为50°;∠CAO是(填“是”或“不是”)∠AOC的同旁内角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
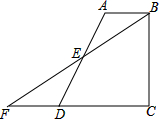 如图,在四边形ABCD中,AB∥CD,BC⊥CD,垂足为点C,E是AD的中点,连接BE并延长交CD的延长线于点F.
如图,在四边形ABCD中,AB∥CD,BC⊥CD,垂足为点C,E是AD的中点,连接BE并延长交CD的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
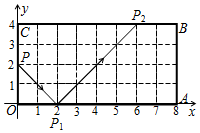 如图,矩形OABC中,OA=8,OC=4,点A、C分别在x轴和y轴上.弹性小球从点P(0,2)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1(2,0),第2次碰到矩形的边时的点为P2,…第n次碰到矩形的边时的点为Pn,则点P2016的坐标是(0,2).
如图,矩形OABC中,OA=8,OC=4,点A、C分别在x轴和y轴上.弹性小球从点P(0,2)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1(2,0),第2次碰到矩形的边时的点为P2,…第n次碰到矩形的边时的点为Pn,则点P2016的坐标是(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
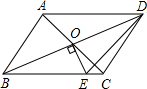 如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E,若△CDE的周长为10,则平行四边形ABCD的周长是多少?
如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E,若△CDE的周长为10,则平行四边形ABCD的周长是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com