
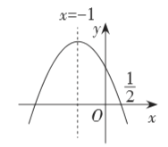
【题目】如图,抛物线![]() 的对称轴是
的对称轴是![]() ,且过点
,且过点![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的结论是______.(填序号)
.其中正确的结论是______.(填序号)
【答案】①③⑤
【解析】
①由图像知![]() ; 由抛物线对称抽是
; 由抛物线对称抽是![]() 得
得![]() ,所以
,所以![]() ,
,![]() ;进而得
;进而得![]() ;
;
②有图像知,抛物线过![]() ,代入抛物线解析式可得
,代入抛物线解析式可得![]() ;
;
③由于![]() 可变形为
可变形为![]() , 而x轴上(
, 而x轴上(![]() ,0)关于
,0)关于![]() 对称的点是(
对称的点是(![]() ,0),所以
,0),所以![]() 正确;
正确;
④因为抛物线与x轴有两个不同的交点,所以![]() ;
;
⑤当![]() 时,抛物线取得最大值
时,抛物线取得最大值![]() ,当
,当![]() 时,则
时,则![]() ,整理可得
,整理可得![]() .
.
解:①由图像知![]() ; 由抛物线对称抽是
; 由抛物线对称抽是![]() 得
得![]() ,所以
,所以![]() ,
,![]() ;进而得
;进而得![]() ;故①正确;
;故①正确;
②有图像知,抛物线过![]() ,代入抛物线解析式整理可得
,代入抛物线解析式整理可得![]() ,故②错误;
,故②错误;
③由于![]() 可变形为
可变形为![]() , 而在x轴上(
, 而在x轴上(![]() ,0)关于
,0)关于![]() 对称的点是(
对称的点是(![]() ,0),故③正确;
,0),故③正确;
④由图像可知,抛物线与x轴有两个不同的交点,所以![]() ,故④错误;
,故④错误;
⑤当![]() 时,抛物线取得最大值
时,抛物线取得最大值![]() ,当
,当![]() 时,则
时,则![]() ,整理可得
,整理可得![]() .故⑤正确.
.故⑤正确.
故答案为:①③⑤.


科目:初中数学 来源: 题型:
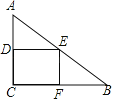
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,矩形CDEF的顶点E在边AB上,D,F两点分别在边AC,BC上,且![]() ,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
A.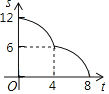 B.
B.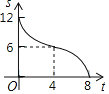 C.
C.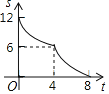 D.
D.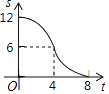
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为3月22日至27日间,我区每日最高气温与最低气温的变化情况.
(1)最低气温的中位数是 ℃;3月24日的温差是 ℃;
(2)分别求出3月22日至27日间的最高气温的平均数、最低气温的平均数;
(3)经过计算,最高气温和最低气温的方差分别为6.33、5.67,数据更稳定的是最高气温还是最低气温?
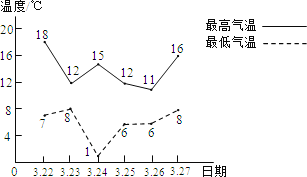
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着![]() 技术的发展,人们对各类
技术的发展,人们对各类![]() 产品的使用充满期待.某公司计划在某地区销售第一款
产品的使用充满期待.某公司计划在某地区销售第一款![]() 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第
产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第![]() (
(![]() 为正整数)个销售周期每台的销售价格为
为正整数)个销售周期每台的销售价格为![]() 元,
元,![]() 与
与![]() 之间满足如图所示的一次函数关系.
之间满足如图所示的一次函数关系.
(1)求![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)设该产品在第![]() 个销售周期的销售数量为
个销售周期的销售数量为![]() (万台),
(万台),![]() 与
与![]() 的关系可用
的关系可用![]() 来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
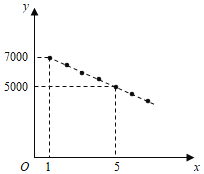
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的动点(与点
上的动点(与点![]() 、
、![]() 不重合),且
不重合),且![]() ,
,![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.
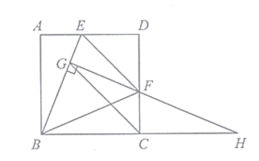
(1)求证:①![]()
![]()
![]() ;②
;②![]() ;
;
(2)若![]() ,在点
,在点![]() 运动过程中,探究:
运动过程中,探究:
①线段![]() 的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
②当![]() 为何值时,
为何值时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
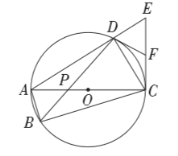
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 是
是![]() 的直径,过点
的直径,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将三角形
将三角形![]() 折叠,得三角形
折叠,得三角形![]() .
.
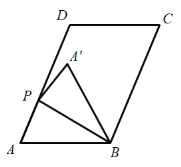
(1)当![]() 时,
时,![]() =_______度;
=_______度;
(2)如图,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 落在平行四边形
落在平行四边形![]() 的边上时,直接写出线段
的边上时,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在OABC中,以O为圆心,OA为半径的圆与BC相切于点B,与OC相交于点D,点E在⊙O上,连接CE与⊙O交于点F.

(1)若BC=20,求![]() 的长度;
的长度;
(2)若EF=AB,求∠OCE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com