
【题目】我市大力发展乡村旅游产业,全力打造客都美丽乡村”,其中“客家美景、客家文化、客家美食”享誉全省,游人络绎不绝.去年我市某村村民抓住机遇,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮收入是住宿收入的2倍还多1万元.
(1)求去年该农家乐餐饮和住宿的收入各为多少万元?
(2)今年该村村民再投入了10万元,增设了土特产的实体销售和网上销售项目并实现盈利,村民在接受记者采访时说,预计今年餐饮和住宿的收入比去年还会有10%的增长.这两年的总收入除去所有投资外还能获得不少于10万元的纯利润,请问今年土特产销售至少收入多少万元?
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M 称为碟顶.
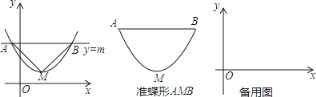
(1)由定义知,取AB中点N,连结MN,MN与AB的关系是_____.
(2)抛物线y=![]() 对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
(3)抛物线y=ax2﹣4a﹣![]() (a>0)对应的碟宽在x 轴上,且AB=6.
(a>0)对应的碟宽在x 轴上,且AB=6.
①求抛物线的解析式;
②在此抛物线的对称轴上是否有这样的点P(xp,yp),使得∠APB为锐角,若有,请求出yp的取值范围.若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整)
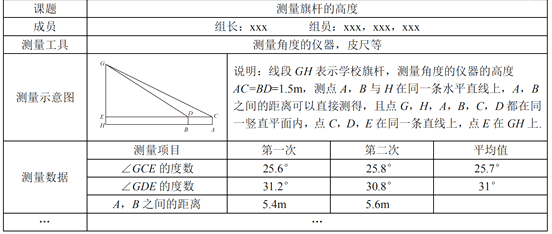

任务一:两次测量A,B之间的距离的平均值是 m.
任务二:根据以上测量结果,请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.
(参考数据:sin25.7°≈0.43,cos25.7°≈0.90,tan25.7°≈0.48,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
任务三:该“综合与实践”小组在定制方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,给定不在同一直线上的点A,B,C,如图所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,![]() 的平分线交图形G于点D,连接AD,CD.
的平分线交图形G于点D,连接AD,CD.
(1)求证:AD=CD;
(2)过点D作DE![]() BA,垂足为E,作DF
BA,垂足为E,作DF![]() BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
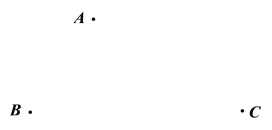
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(2m+1)x﹣3m.
(1)若m=2,写出该函数的表达式,并求出函数图象的对称轴.
(2)已知点P(m,y1),Q(m+4,y2)在该函数图象上,试比较y1,y2的大小.
(3)对于此函数,在﹣1≤x≤1的范围内至少有x值使得y≥0,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
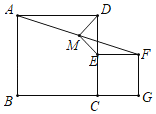
【题目】如图,已知正方形ABCD与正方形CEFG,点E在CD上,点G在BC的延长线上,M是AF的中点,连接DM,EM.
(1)填空:DM与EM数量关系和位置关系为 (直接填写);
(2)若AB=4,设CE=x(0<x<4),△MEF面积为y,求y关于x的函数关系式[可利用(1)的结论],并求出y的最大值;
(3)如果将正方形CEFG绕点C顺时针旋转任意角度,我们发现DM与EM数量关系与位置关系仍未发生改变.
①若正方形ABCD边长AB=13,正方形CEFG边长CE=5,当D,E,F三点旋转至同一条直线上时,求出MF的长;
②证明结论:正方形CEFG绕点C顺时针旋转任意角度,DM与EM数量关系与位置关系仍未发生改变.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=4,tan∠ABD=![]() ,求BE的长.
,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统汁图,请根据图中信息解答下列问题:
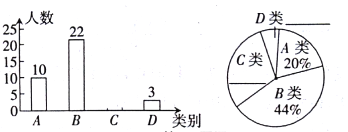
(l)本次抽取样本容量为____,扇形统计图中A类所对的圆心角是____度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
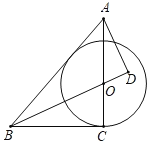
【题目】如图,在△ABC中,O为AC上一点以O为圆心,OC长为半径作圆,与BC相切于点C,过点A作AD⊥BO交BO延长线于点D,且∠AOD=∠BAD.
(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC![]() ,求OD的长.
,求OD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com