

���� ��1����������ͳ��ͼ�ɵã�����ͳ��ͼ�����߲��֣��ݴ˼����жϣ�
��2����������ͳ��ͼ����ֱ����⣻
��3������ʵ������ͳ��ͼ����ֱ����⣻
��4��������������Զ�Ӧ�İٷֱȼ�����⣮
��� �⣺��1��ȫ���繲���߸����ޣ�����������
��2�����ޡ����������������֮����ӽ�������½�������һ�룻
��3��ͼ�и������ηֱ������ÿ��������ռ�İٷֱȣ����аٷֱ�֮����1��
��4������ı����Ϊ5.1��ƽ��ǧ�ף���½�����Ϊ1.49��ƽ��ǧ�ף�
��ռ��������������29.2%��������½�����ԼΪ4.3657��103��ƽ��ǧ�ף��ÿ�ѧ��������ʾ������ռ����ı����ԼΪ8.56%��
���� ���⿼���������ͳ��ͼ�����ã�����ͳ��ͼ����ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ�������ͳ��ͼֱ�ӷ�ӳ����ռ����İٷֱȴ�С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
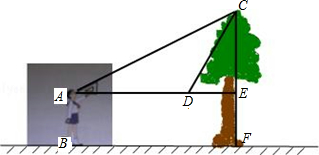 ��ͼ��С��ͬѧ�����һ�ô����ĸ߶ȣ���վ��B�������������������Ϊ30�㣬���������ķ���ǰ��4m���������Ϊ60�㣬��֪С��ͬѧ����ABΪ1.7m����������ĸ߶ȣ��������ȷ��0.1m��$\sqrt{3}$��1.73��
��ͼ��С��ͬѧ�����һ�ô����ĸ߶ȣ���վ��B�������������������Ϊ30�㣬���������ķ���ǰ��4m���������Ϊ60�㣬��֪С��ͬѧ����ABΪ1.7m����������ĸ߶ȣ��������ȷ��0.1m��$\sqrt{3}$��1.73���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| a | b | c | a+b-c | $\frac{s}{l}$ |
| 3 | 4 | 5 | 2 | $\frac{1}{2}$ |
| 5 | 12 | 13 | 4 | 1 |
| 8 | 15 | 17 | 6 | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
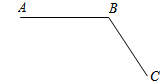 ��ͼ��ƽ������A��B��C���㣮
��ͼ��ƽ������A��B��C���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{8a}$ | B�� | $\sqrt{5a}$ | C�� | $\sqrt{0.5x}$ | D�� | $\sqrt{{a}^{2}+{a}^{2}b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{1}{2}x}$ | B�� | $\sqrt{18x}$ | C�� | $\sqrt{3x}$ | D�� | $\sqrt{{x}^{2}y}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{8}$ | B�� | $\sqrt{14}$ | C�� | $\sqrt{\frac{1}{2}}$ | D�� | $\sqrt{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a8-b8 | B�� | a8-2a4b4+b8 | C�� | a8+b8 | D�� | a8+2a4b4+b8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com