
分析 (1)由“每月游客人数控制在200人以内”知y<200,据此列不等式求解可得;
(2)根据“总成本=每人的成本价×游客人数”可得函数解析式,据此根据一次函数性质可得;
(3)根据“总利润=每人的利润×游客人数”得出总利润关于报价的函数解析式,配方成顶点式,利用二次函数的性质可得其最值情况.
解答 解:(1)由题意得y<200时,即-x+1300<200,
解得:x>1100,
即该旅游线路报价的取值范围为1100元/人~1200元/人之间;
(2)设经营这条旅游线路每月所需要的成本为z,
∴z=500(-x+1300)=-500x+650000,
∵-500<0,
∴当x=1200时,z最低,即z=50000;
(3)设经营这条旅游线路的总利润为w,
则w=(x-500)(-x+1300)=-x2+1800x-650000=-(x-900)2+160000,
当x=900时,w最大=160000.
点评 本题主要考查二次函数的应用,解题的关键是根据题意确定相等关系,并据此列出函数解析式.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
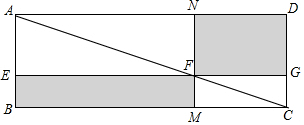 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com