

分析 (1)根据三角形相似的判定,证明△MAF∽△EDF,进而用含t的式子表示MA,再根据平行四边形的性质,得MA=DE,求出t的值即可;
(2)根据题意,分0≤t≤$\frac{5}{2}$和$\frac{5}{2}$<t≤4两种情况解答,根据整体减去部分的方法求出面积即可;
(3)要使△BEF是等腰三角形,只要满足BE=BF即可,根据全等即可求出t的值.
解答 解:(1)如图①,
在?ABCD中,AB=CD=4cm,AD=5cm,AB∥CD,
∴∠MAF=∠EDF,
∵∠MFA=∠EFD,
∴△MAF∽△EDF,
∴$\frac{MA}{AF}=\frac{DE}{DF}$,即$\frac{MA}{2t}=\frac{4-t}{5-2t}$,解得:MA=$\frac{2t(4-t)}{5-2t}$,
要使四边形AMDE是平行四边形,只要满足MA=DE即可,即$\frac{2t(4-t)}{5-2t}=4-t$,整理,得:4t2-21t+20=0,
解得:${t}_{1}=\frac{5}{4}$,t2=4(不合题意,舍去),
∴当$t=\frac{5}{4}$时,四边形AMDE是平行四边形.
(2)∵AB⊥BD,AD=5cm,AB=4cm,
∴BD=$\sqrt{A{D}^{2}-A{B}^{2}}=\sqrt{{5}^{2}-{4}^{2}}=3$cm,
当0≤t≤$\frac{5}{2}$时,如图②,
过点F作FG⊥CD的延长线于点G,FH⊥AB于点H,
则GH=3cm,△AFH∽△DFG,
∴$\frac{FH}{FG}=\frac{AF}{DF}$,即$\frac{FH}{3-FH}=\frac{2t}{5-2t}$,解得:FH=$\frac{6}{5}$t,FG=3-$\frac{6}{5}$t,
∴S四边形BCEF=S?ABCD-S△EDF-S△ABF=4×3-$\frac{1}{2}$×DE×FG-$\frac{1}{2}$×AB×FH=$-\frac{3}{5}{t}^{2}+\frac{3}{2}t+12$;
当$\frac{5}{2}$<t≤4时,如图③,
∴S四边形BCEF=S△BCD-S△EDF=$\frac{1}{2}$×3×4-$\frac{1}{2}$×ED×DF=${t}^{2}-\frac{13}{2}t+16$,
综上所述,y=$\left\{\begin{array}{l}{-\frac{3}{5}{t}^{2}+\frac{3}{2}t+12(0≤t≤\frac{5}{2})}\\{{t}^{2}-\frac{13}{2}t+16(\frac{5}{2}<t≤4)}\end{array}\right.$.
(3)当t=1时,△BEF是等腰三角形.
点评 本题主要考查四边形、三角形的相关知识,第(1)小题,要熟练掌握相似三角形的性质和判定;第(2)小题,分两种情况讨论是解决此题对关键;第(3)小题,需要熟练掌握等腰三角形的判定方法.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 与三角形的一边和其他两边的延长线都相切的圆叫做这个三角形的旁切圆,其圆心叫做这个三角形的旁心.如图,△ABC的三个顶点的坐标分别为A(-3,0),B(3,0),C(0,4).则△ABC位于第二象限的旁心D的坐标是(-5,4).
与三角形的一边和其他两边的延长线都相切的圆叫做这个三角形的旁切圆,其圆心叫做这个三角形的旁心.如图,△ABC的三个顶点的坐标分别为A(-3,0),B(3,0),C(0,4).则△ABC位于第二象限的旁心D的坐标是(-5,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -29a10 | B. | 29a10 | C. | 210a10 | D. | -210a10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等腰直角△ABC中,AC=BC,AD⊥AB(点D在AB的右上方),E为AB边上一点,且BE=4,DE=6,当CD平分∠ADE时,CE的长度为2$\sqrt{6}$.
如图,在等腰直角△ABC中,AC=BC,AD⊥AB(点D在AB的右上方),E为AB边上一点,且BE=4,DE=6,当CD平分∠ADE时,CE的长度为2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
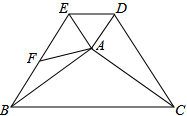 如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.
如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com