
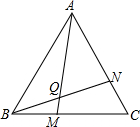
 ѧ�ꡰ��Գơ���һ�º���ʦ������һ��˼���⣺��ͼ��ʾ����M��N�ֱ��ڵȱߡ�ABC��BC��CA���ϣ���BM=CN��AM��BN���ڵ�Q����֤����BQM=60��
ѧ�ꡰ��Գơ���һ�º���ʦ������һ��˼���⣺��ͼ��ʾ����M��N�ֱ��ڵȱߡ�ABC��BC��CA���ϣ���BM=CN��AM��BN���ڵ�Q����֤����BQM=60������ ��1��ֻҪ֤����ABM�ա�BCN��SAS�����Ƴ���BAM=��CBN���ɵá�BQM=��BAQ+��ABQ=��MBQ+��ABQ=60�㣻
��2�����������⣬֤���������ƣ�
���������⣮֤���������ƣ�
���Ǽ����⣬֤���������ƣ�
��� �⣺��1���ߡ�ABCΪ�ȱ������Σ�
��AB=BC=AC����BAC=��ABC=��ACB=60�㣬
�ڡ�ABM�͡�BCN�У�
��BM=CN����ABM=��BCN��AB=BC��
���ABM�ա�BCN��SAS����
���BAM=��CBN��
���BQM=��BAQ+��ABQ=��MBQ+��ABQ=60�㣻
��2�����ǣ����ǣ��۷�
����֪����BQM=60�㣬��֤��BM=CN��
֤�����ߡ�BQM=��ABM=60�㣬��BMQ=��AMB��
���BMQ�ס�AMB�����CBN=��BAM��
�ڡ�ABM�͡�BCN�У�
�ߡ�BAM=��CBN��AB=BC����ABM=��BCN�����ABM�ա�BCN��ASA����
��BM=CN��
��֤������ͼ��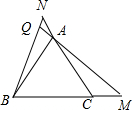
�ڡ�ACM�͡�BAN�У�
��CM=AN����ACM=��BAN=120�㣬AC=AB�����ACM�ա�BAN��SAS����
���AMC=��BNA�����NQA=��NBC+��BMQ=��NBC+��BNA=180��-60��=120�㣬
���BQM=60�㣻
��֤������ͼ��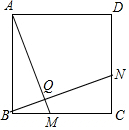
��Rt��ABM��Rt��BCN��
��BM=CN��AB=BC��
��Rt��ABM��Rt��BCN��HL����
���AMB=��BNC��
�֡ߡ�NBM+��BNC=90�㣬
���QBM+��QMB=90�㣬���BQM=90�㣮
�ʴ�Ϊ�����ǣ����ǣ��۷�
���� ���⿼��ȱ������ε����ʡ������ε����ʡ�ȫ�������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬�����п��������ͣ�


 ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
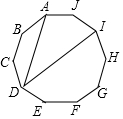 ��ͼ������ʮ����ABCDEFGHIJ�У�AD��DI�������Խ��ߣ����ADI=36�㣮
��ͼ������ʮ����ABCDEFGHIJ�У�AD��DI�������Խ��ߣ����ADI=36�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 8 | C�� | 7 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
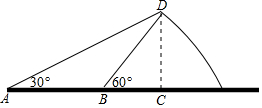 ��ͼ����ɽ���µ�һ��A���ɽ��D��������30�㣬��Aǰ��100��B���ٴβ��ɽ��D������Ϊ60�㣬��ɽ��CD�ĸ߶ȣ������ȷ��0.1�ף������ο����ݣ�$\sqrt{2}$��1.414��$\sqrt{3}$��1.732��
��ͼ����ɽ���µ�һ��A���ɽ��D��������30�㣬��Aǰ��100��B���ٴβ��ɽ��D������Ϊ60�㣬��ɽ��CD�ĸ߶ȣ������ȷ��0.1�ף������ο����ݣ�$\sqrt{2}$��1.414��$\sqrt{3}$��1.732���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com