
分析 (1)先根据完全平方公式和平方平方差公式展开,再合并即可;
(2)变形后提公因式,再用平方差公式分解即可;
(3)先算括号内的减法,再把除法变成乘法,化简后代入求出即可.
解答 解:(1)原式=($\sqrt{2}$)2-2×$\sqrt{2}$×$\sqrt{3}$+($\sqrt{3}$)2+(2$\sqrt{3}$)2-($\sqrt{6}$)2
=2-2$\sqrt{6}$+3+12-6
=11-2$\sqrt{6}$;
(2)原式=9a2(x-y)-4b2(x-y)
=(x-y)(9a2-4b2)
=(x-y)(3a+2b)(3a-2b);
(3)$\frac{a-2}{{a}^{2}-1}$÷(a-1-$\frac{2a-1}{a+1}$)
=$\frac{a-2}{{a}^{2}-1}$÷$\frac{(a-1)(a+1)-(2a-1)}{a+1}$
=$\frac{a-2}{{a}^{2}-1}$÷$\frac{{a}^{2}-2a}{a+1}$
=$\frac{a-2}{(a+1)(a-1)}$•$\frac{a+1}{a(a-2)}$
=$\frac{1}{a(a-1)}$
=$\frac{1}{{a}^{2}-a}$,
∵a2-a-6=0,
∴a2-a=6,
∴原式=$\frac{1}{6}$.
点评 本题考查了分解因式,二次根式的混合运算,分式的混合运算和求值的应用,能熟记各个知识点是解此题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:选择题
 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴于点C和点D,则DC的长为( )
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴于点C和点D,则DC的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
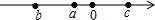 已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$-$\sqrt{(a-c)^{2}}$-$\sqrt{(b-c)^{2}}$的结果是( )
已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$-$\sqrt{(a-c)^{2}}$-$\sqrt{(b-c)^{2}}$的结果是( )| A. | -3a | B. | -a+2b-2c | C. | 2b | D. | a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若
如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点A、B在双曲线y=$\frac{m}{x}$(m>0)上,点C、D在双曲线y=$\frac{n}{x}$(n<0)上,
如图,已知点A、B在双曲线y=$\frac{m}{x}$(m>0)上,点C、D在双曲线y=$\frac{n}{x}$(n<0)上,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=x2+bx+c(x为整数).若l经过这九个格点中的三个,直接写出所有满足这样条件的抛物线条数有4条.
如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=x2+bx+c(x为整数).若l经过这九个格点中的三个,直接写出所有满足这样条件的抛物线条数有4条.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com