
已知关于x的一元二次方程x²+2(m-2)x+m²+4=0的两实数根是 和
和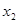 .
.
(1)求m的取值范围;
(2)如果 ²+
²+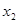 ²-
²-
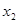 =21 ,求m的值.
=21 ,求m的值.
详见解析
【解析】
试题分析:(1)m的取值范围,可由一元二次方程的根的判别式构建不等式求解。因为原方程有两实数根,所以△=b2-4ac≥0,将a、b、c代入解不等式即可求解。
利用一元二次方程的根与系数的关系,是解题的关键.由根与系数的关系可知:x1+x2=-2(m-2)=4-2m,
x1·x2=m²+4,利用配方法把原方程化为一元二次方程的一般形式,即(x1+x2)2-3x1·x2-21=0.所以(4-2m)2-3(m²+4)-21=0,解方程求解,再利用m的取值范围确定m的取值.
试题解析:
解:(1)∵方程由两个实数根
∴△=b²-4ac=4﹙m-2﹚²-4﹙m²+4﹚≥0
∴m≤0
(2)由根与系数的关系知:x1+x2=﹣2(m-2)=4-2m,x1·x2=m²+4
∵ x1²+x2²-x1·x2=21
∴﹙x1+x2﹚²-3x1·x2=21
∴4﹙m-2﹚²-3﹙m²+4﹚=21
m²-16m-17=0
﹙m-17﹚﹙m+1﹚=0
m1=17,m2=﹣1
∵m≤0
∴m=﹣1
考点:一元二次方程根与系数的关系


 同步轻松练习系列答案
同步轻松练习系列答案科目:初中数学 来源:第23章《一元二次方程》中考题集(23):23.3 实践与探索(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《一元二次方程》(04)(解析版) 题型:解答题
 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com