
 π,求线段AM的长;
π,求线段AM的长;
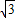 ,然后根据直线过M点,而OM可以在直角三角形AMO中求出,也就能得出M的坐标,然后用待定系数法求出函数的解析式,这样,可根据矩形的面积公式,以N的横坐标的绝对值当矩形的宽,以N的纵坐标的绝对值当矩形的长,以此可得出关于矩形的面积与横坐标的函数关系式,然后根据函数的性质判定出x为什么值时,矩形的面积最大,然后将x的值代入AM所在直线的解析式中得出N点的坐标.
,然后根据直线过M点,而OM可以在直角三角形AMO中求出,也就能得出M的坐标,然后用待定系数法求出函数的解析式,这样,可根据矩形的面积公式,以N的横坐标的绝对值当矩形的宽,以N的纵坐标的绝对值当矩形的长,以此可得出关于矩形的面积与横坐标的函数关系式,然后根据函数的性质判定出x为什么值时,矩形的面积最大,然后将x的值代入AM所在直线的解析式中得出N点的坐标.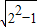 =
=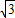 ,依题意有:
,依题意有: ×2
×2 π×2+
π×2+ ×2
×2 π×AM=5
π×AM=5 π,∴AM=3;
π,∴AM=3;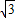 ,AM=3,
,AM=3,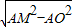 =
= ,
, ,0),设直线AM的解析式为:y=kx+
,0),设直线AM的解析式为:y=kx+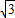 ,
,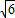 ,0),
,0),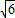 k+
k+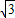 =0,k=-
=0,k=-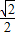 ,
, x+
x+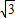 .设点N的坐标为(x,y),
.设点N的坐标为(x,y), x+
x+ )=-
)=- x2+
x2+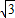 x=-
x=-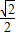 (x-
(x-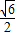 )2+
)2+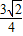 ,
, 时,矩形NGOH的面积取得最大值,
时,矩形NGOH的面积取得最大值,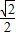 x+
x+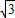 =
=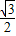 ,
, ,
, ).
).

科目:初中数学 来源:2007年全国中考数学试题汇编《图形的对称》(04)(解析版) 题型:解答题
 π,求线段AM的长;
π,求线段AM的长;
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《圆》(14)(解析版) 题型:解答题
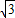 π,求线段AM的长;
π,求线段AM的长;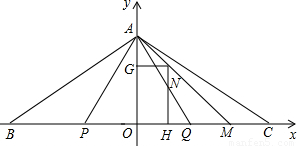
查看答案和解析>>
科目:初中数学 来源:2007年广西桂林市中考数学试卷(解析版) 题型:解答题
 π,求线段AM的长;
π,求线段AM的长;
查看答案和解析>>
科目:初中数学 来源:2007年广西桂林市中考数学试卷(解析版) 题型:解答题
 ,土坝与地面的倾角∠ABC=60度,要改造100米长的护坡土坝,选择哪家施工队所需费用较少?
,土坝与地面的倾角∠ABC=60度,要改造100米长的护坡土坝,选择哪家施工队所需费用较少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com