
【题目】实践活动小组要测量旗杆的高度,现有标杆、皮尺.小明同学站在旗杆一侧,通过观视和其他同学的测量,求出了旗杆的高度,请完成下列问题:
(1)小明的站点![]() ,旗杆的接地点
,旗杆的接地点![]() ,标杆的接地点
,标杆的接地点![]() ,三点应满足什么关系?
,三点应满足什么关系?
(2)在测量过程中,如果标杆的位置确定,小明应该通过移动位置,直到小明的视点![]() 与点 在同直一线上为止;
与点 在同直一线上为止;
(3)他们都测得了哪些数据就能计算出旗杆的高度?请你用小写字母表示这些数据(不允许测量多余的数据);
(4)请用(3)中的数据,直接表示出旗杆的高度.

【答案】![]()
![]() 三点在同一条直线上;
三点在同一条直线上;![]()
![]() 和点
和点![]() ;
;![]() 答案不唯一:测量
答案不唯一:测量![]() 的长就能计算出旗杆的高度,设测得
的长就能计算出旗杆的高度,设测得![]() ;
;![]()
![]()
【解析】
过C点作DB的平行线,与EF交于M点,与AB交于N点,测量旗杆高是根据△CME∽△CNA进行计算的,所以(1)小明的站点![]() ,旗杆的接地点
,旗杆的接地点![]() ,标杆的接地点
,标杆的接地点![]() ,三点必须在同一直线上;(2)在测量过程中,如果标杆的位置确定,小明应该通过移动位置,直到小明的视点
,三点必须在同一直线上;(2)在测量过程中,如果标杆的位置确定,小明应该通过移动位置,直到小明的视点![]() 点与A、E点都在同直一线上为止;(3)根据相似三角形成比例测量
点与A、E点都在同直一线上为止;(3)根据相似三角形成比例测量![]() 的长就能计算出旗杆的高度,设测得
的长就能计算出旗杆的高度,设测得![]() ;(4)根据△CME∽△CAN,写出比例式
;(4)根据△CME∽△CAN,写出比例式![]() ,表示出AN,然后AB=AN+BN即可得到答案
,表示出AN,然后AB=AN+BN即可得到答案
如图,过C点作DB的平行线,与EF交于M点,与AB交于N点
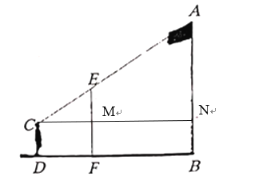
(1)小明的站点![]() ,旗杆的接地点
,旗杆的接地点![]() ,标杆的接地点
,标杆的接地点![]() ,三点必须在同一直线上;
,三点必须在同一直线上;
(2)在测量过程中,如果标杆的位置确定,小明应该通过移动位置,直到小明的视点![]() 点与A、E点都在同直一线上为止;
点与A、E点都在同直一线上为止;
(3)根据相似三角形成比例测量![]() 的长就能计算出旗杆的高度,设测得
的长就能计算出旗杆的高度,设测得![]() ;
;
(4)易知△CME∽△CAN,有![]() ,CM=DF=c,EM=EF-MF=b-a,CN=DF+FB=c+d,即有
,CM=DF=c,EM=EF-MF=b-a,CN=DF+FB=c+d,即有![]() ,解得AN=
,解得AN=![]() ,所以AB=
,所以AB=![]()


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
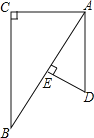
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美是一种感觉,本应没有什么客观的标准,但在自然界里,物体形状的比例却提供了在的称与协调上的一种美感的参考,在数学上,这个比例称为黄金分割.在人体由脚底至肚脐的长度与身高的比例上,肚脐是理想的黄金分割点,也就是说,若此比值越接近![]() 就越给别人一种美的感觉. 某女士身高为
就越给别人一种美的感觉. 某女士身高为![]() ,脚底至肚脐的长度与身高的比为
,脚底至肚脐的长度与身高的比为![]() 为了追求美,地想利用高跟鞋达到这一效果 ,那么她选的高跟鞋的高度约为( )
为了追求美,地想利用高跟鞋达到这一效果 ,那么她选的高跟鞋的高度约为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4、5、6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为53°和45°,已知大桥BC与地面在同一水平面上,其长度为75m,请求出热气球离地面的高度.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() ).
).
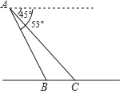
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
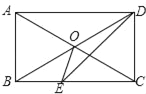
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com