
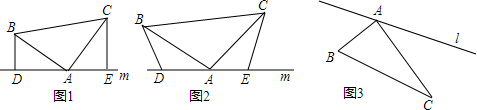
分析 (1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
(2)利用∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°-α,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案;
(3)易证∠PFA=∠QGA,∠PAF=∠AQG,只需PA=QA,就可得到△PFA与△QAG全等,然后只需根据点P和点Q不同位置进行分类讨论即可解决问题.
解答 证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠CEA}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠CEA}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
(3)①当0≤t<$\frac{28}{3}$时,点P在AB上,点Q在AC上,
此时有BF=2t,CG=3t,AB=22,AC=28.
当PA=QA即22-2t=28-3t,也即t=6时,
∵PF⊥l,QG⊥l,∠BAC=90°,
∴∠PFA=∠QGA=∠BAC=90°.
∴∠PAF=90°-∠GAQ=∠AQG.
在△PFA和△QAG中,
$\left\{\begin{array}{l}{∠PFA=∠QGA}\\{∠PAF=∠AQG}\\{PA=QA}\end{array}\right.$,
∴PFA与≌QAG(AAS).
②当$\frac{28}{3}$≤t<11时,点P在AB上,点Q也在AB上,
此时相当于两点相遇,则有2t+3t=50,解得t=10;
③当7<t<18时,点Q停在点B处,点P在AC上,
当PA=QA即2t-22=22,解得t=22(舍去).
综上所述:当t等于6或10时,△PFA与△QAG全等.
点评 本题考查了全等三角形的判定与性质以及分类讨论的思想,可能会因考虑不全面而出错,是一道易错题.判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;得出∠CAE=∠ABD是解题关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
| 采购部 | 经理,这里有一批商品以每件42元购回 |
| 销售部 | 经理,以每件42元购回的商品,每天的销售量t(件)与每件的销售价x(元)呈现的关系是:t=-3x+204 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明要在一幅长90厘米、宽40厘米的风景画的四周外围镶上一个宽度相同的边框,制成一挂图,使风景画的面积为整个挂图面积的54%.设边框的宽度为x厘米,根据题意所列方程是(90+2x)(40+2x)×54%=90×40.
如图,小明要在一幅长90厘米、宽40厘米的风景画的四周外围镶上一个宽度相同的边框,制成一挂图,使风景画的面积为整个挂图面积的54%.设边框的宽度为x厘米,根据题意所列方程是(90+2x)(40+2x)×54%=90×40.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=6时,这两个二次函数的最大值之和等于( )
如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=6时,这两个二次函数的最大值之和等于( )| A. | 5 | B. | $\frac{{8\sqrt{5}}}{3}$ | C. | 10 | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com