
分析 (1)用配方法解一元二次方程即可;
(2)用公式法求解即可;
(3)用公式法求解即可;
(4)先整理成一般形式,再用因式分解法解方程即可;
(5)先整理成一般形式,再用因式分解法解方程即可.
解答 解:(1)a=1,b=-6,c=4,
△=b2-4ac=36-16=20>0,
∴方程有两个不相等的实数根,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{6±\sqrt{20}}{2}$=3±$\sqrt{5}$,
∴x1=3+$\sqrt{5}$,x2=3-$\sqrt{5}$;
(2)整理得,2x2+5x-3=0,
a=2,b=5,c=-3,
△=b2-4ac=25+24=49>0,
∴方程有两个不相等的实数根,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-5±\sqrt{49}}{4}$,
∴x1=-3,x2=$\frac{1}{2}$.
(3)a=3,b=-2$\sqrt{3}$,c=-3,
△=b2-4ac=12+36=48>0,
∴方程有两个不相等的实数根,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{2\sqrt{3}±\sqrt{48}}{6}$,
∴x1=$\sqrt{3}$,x2=-$\frac{\sqrt{3}}{3}$;
(4)2x2+5x-8=0,
a=2,b=5,c=-8,
△=b2-4ac=25+64=89>0,
∴方程有两个不相等的实数根,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{5±\sqrt{89}}{4}$,
∴x1=$\frac{5+\sqrt{89}}{4}$,x2=$\frac{5-\sqrt{89}}{4}$;
(5)y2+6y+4=2y2-4y-7.
y2-10y-11=0,
(y+1)(y-11)=0,
y+1=0或y-11=0,
∴y1=-1,y2=11.
点评 本题考查了解一元二次方程,掌握解一元二次方程的方法:配方法、公式法、因式分解法是解题的关键.


科目:初中数学 来源:2016-2017学年湖北省枝江市九校七年级3月联考数学试卷(解析版) 题型:单选题
如图,直线a,b相交于点O,若∠1等于40°,则∠2等于( )
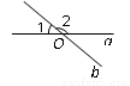
A. 50° B. 60° C. 140° D. 160°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 收缩压的变化 (与前一天相比) | 升30单位 | 降20单位 | 升17单位 | 升18单位 | 降20单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com