
【题目】如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F.求证:(1)△ACE≌△BCD;(2)![]() .
.

【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)由三角形ABC与三角形CDE都为等边三角形,利用等边三角形的性质得到两对边相等,一对角相等,利用等式的性质得到夹角相等,利用SAS即可得证;
(2)由(1)得出的三角形全等得到对应角相等,再由一对角相等,且夹边相等,利用ASA得到三角形GCD与三角形FCE全等,利用全等三角形对应边相等得到CG=CF,进而确定出三角形CFG为等边三角形,确定出一对内错角相等,进而得到GF与CE平行,利用平行线等分线段成比例即可得证.
试题解析:解:(1)∵△ABC与△CDE都为等边三角形,∴AC=BC,CE=CD,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD.在△ACE和△BCD中,∵AC=BC,∠ACE=∠BCD,CE=CD,∴△ACE≌△BCD(SAS);
(2)∵△ACE≌△BCD,∴∠BDC=∠AEC.在△GCD和△FCE中,∵∠GCD=∠FCE=60°,CD=CE,∠BDC=∠AEC,∴△GCD≌△FCE(ASA),∴CG=CF,∴△CFG为等边三角形,∴∠CGF=∠ACB=60°,∴GF∥CE,∴ ![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
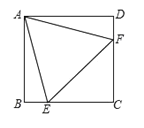
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点![]() 分别在BC和CD上,下列结论:
分别在BC和CD上,下列结论:
(1)BE=DF;(2)∠AEB=75°;(3)BE+DF=EF;(4)![]() .
.
其中正确的序号是____________(把你认为正确的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=![]() , CF=3,求DF的长.
, CF=3,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
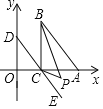
【题目】如图,在直角坐标系中,三角形![]() 两顶点的坐标为
两顶点的坐标为![]() ,
,![]() ,点
,点![]() 是
是![]() 轴上一动点(不与点
轴上一动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() ,
,![]() 分别平分
分别平分![]() .
.
(1)当点![]() 在点
在点![]() 左边,三角形
左边,三角形![]() 的面积为6时,求点
的面积为6时,求点![]() 的坐标.
的坐标.
(2)当![]() 轴时,求
轴时,求![]() 的度数.
的度数.
(3)当点![]() 在点
在点![]() 右边时,写出
右边时,写出![]() 与
与![]() 的数量关系(不用说理).
的数量关系(不用说理).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.

(1)求证:四边形ADCF是菱形;
(3)若AC=6,AB=8,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)的函数图象如图所示.
(时)的函数图象如图所示.

(1)求甲车距离A地的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)之间的函数关系式;
(时)之间的函数关系式;
(2)当x=2.8时,甲、乙两车之间的距离是 千米;乙车到达B地所用的时间![]() 的值为 ;
的值为 ;
(3)行驶过程中,两车出发多长时间首次后相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在防疫知识普查考试中,某次测试试题的满分为20分,某校为了解该校部分学生的成绩情况,从该校七,八年级学生中各随机抽取了20名学生的成绩进行了整理、描述和分析,下面给出了部分信息:
抽取的七年级成绩是:20 20 20 20 19 19 19 19 18 18 18 18 18 18 18 17 16 16 15 14

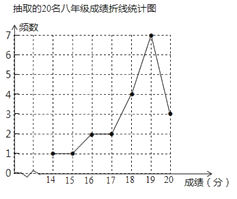
根据以上信息,解答下列问题:
(1)直接写出上表中a,b,c的值;
(2)在这次测试中,你认为是七年级的成绩好,还是八年级成绩好?请说明理由;
(3)该校七、八年级共有学生1000人,估计此次测试成绩不低于19分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com