
【题目】阅读以下材料,并按要求完成相应的任务.
课题学习:如何解一元二次不等式?
例题:解一元二次不等式![]() .
.
解:![]()
![]() .
.
由有理数的乘法法则“两数相乘,同号得正”,有:
![]()
![]()
解不等式组![]() 得:
得:![]()
解不等式组![]() 得:
得:![]()
![]() 的解集为
的解集为![]() 或
或![]() .
.
即:一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
任务:(1)上面解一元二次不等式的过程中体现出了数学的一些基本思想方法,请在下列选项中选出你认为正确的一项:_____ ;(填选项即可)
A.分类讨论思想;B.数形结合思想;C.公理化思想;D.函数思想
(2)求一元二次不等式![]() 的解集为:_____ ;(直接填写结果,不写解答过程)
的解集为:_____ ;(直接填写结果,不写解答过程)
(3)仿照例题中的数学思想方法,求分式不等式![]() 的解集.
的解集.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3) ![]() ;
;
【解析】
(1)根据解题过程可得分为同正、同负两类进行讨论,问题得解;
(2)类比例题解题过程,根据有理数的乘法法则“两数相乘,同号得正”分类讨论,求出不等式组的解集即可;
(3)类比例题,根据有理数的除法法则“两数相除,异号得负”分类讨论,求出不等式组的解集即可.
解:(1)上面解题过程中根据有理数的乘法法则“两数相乘,同号得正”,分为同正和同负两种情况进行,故选![]() ;
;
(2)由有理数的乘法法则“两数相乘,同号得正”,有:
![]()
![]()
解不等式组![]() 得:
得:![]()
解不等式组![]() 得:
得:![]()
∴![]() 的解集为
的解集为![]() 或
或![]() ;
;
(3)由有理数的除法法则“两数相除,异号得负”,有
![]() ,
,![]() ,
,
解不等式组![]() 得:无解,
得:无解,
解不等式组![]() 得:
得:![]()
![]() 分式不等式
分式不等式![]() 的解集为:
的解集为:![]() .
.


科目:初中数学 来源: 题型:
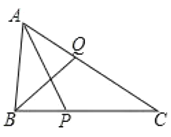
【题目】如图,在△ABC中,∠BAC=60°,∠C=40°,P,Q分别在BC,CA上,AP,BQ分别是∠BAC,∠ABC的角平分线.求证:BQ+AQ=AB+BP.
查看答案和解析>>
科目:初中数学 来源: 题型:
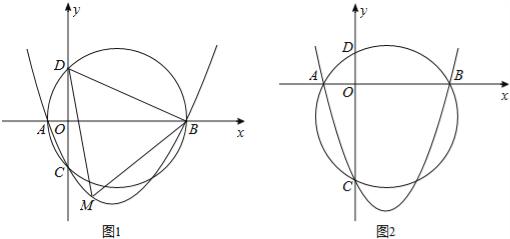
【题目】如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实立德树人根本任务,培养德智体美劳全面发展的社会主义接班人,育才学校在设立学生奖学金时规定:每学期对学生的德智体美劳五个方面进行三次综合素质评价,分别是:假期综合素质评价、期中综合素质评价、期末综合素质评价,八年级(1)班的小明和八年级(2)班的小亮两位同学同时进入一等奖学金测评,他们的三次综合素质评价成绩如下表.
假期综合素质评价成绩 | 期中综合素质评价成绩 | 期末综合素质评价成绩 | |
小明 | 96 | 91 | 92 |
小亮 | 95 | 93 | 91 |
(1)如果从三次综合素质评价成绩稳定性的角度来看,谁可以得一等奖学金?请你通过计算回答;
(2)如果假期综合素质评价成绩、期中综合素质评价成绩、期末综合素质评价成绩按![]() 的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答.
的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答.
查看答案和解析>>
科目:初中数学 来源: 题型:
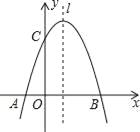
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
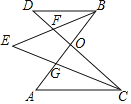
【题目】如图所示,AB、CD相交于点O,若BE平分∠ABD交CD于F,CE平分∠ACD交AB于G,∠A=45°,∠BEC=40°,则∠D的度数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在长方形ABCD中,AB=8cm,BC=12cm,E为AB的中点,动点P在线段BC上以4cm/s的速度由点B向C运动,同时,动点Q在线段CD上由点C向点D运动,设运动时间为t(s).
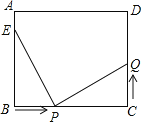
(1)当t=2时,求△EBP的面积;
(2)若动点Q以与动点P不同的速度运动,经过多少秒,△EBP与△CQP全等?此时点Q的速度是多少?
(3)若动点Q以(2)中的速度从点C出发,动点P以原来的速度从点B同时出发,都逆时针沿长方形ABCD的四边形运动,经过多少秒,点P与点Q第一次在长方形ABCD的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,求大树CD的高度?(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
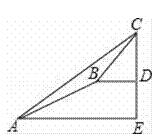
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com