
分析 (1)先根据题意得出x2=4x-1,再根据负整数指数幂的运算法则把原式进行化简,再把x2的值代入进行计算即可;
(2)根据负整数指数幂的运算法则把原式进行化简,再把(1)中的结果代入进行计算即可.
解答 解:(1)∵x2-4x+1=0,
∴x2=4x-1,
∴x2+x-2
=x2+$\frac{1}{{x}^{2}}$
=$\frac{{x}^{4}+1}{{x}^{2}}$
=$\frac{(4x-1)^{2}+1}{4x-1}$
=$\frac{16{x}^{2}-8x+1+1}{4x-1}$
=$\frac{16(4x-1)-8x+2}{4x-1}$=$\frac{64x-16-8x+2}{4x-1}$
=$\frac{56x-14}{4x-1}$
=$\frac{14(4x-1)}{4x-1}$
=14;
(2)x4+x-4
=x4+$\frac{1}{{x}^{4}}$
=(x2+$\frac{1}{{x}^{2}}$)2-2
=142-2
=194.
点评 本题考查的是负整数指数幂,熟知负整数指数幂等于对应的正整数指数幂的倒数是解答此题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
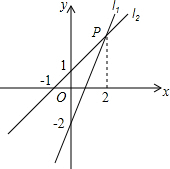 如图,过点(0,-2)的直线l1:y=kx+b(k≠0)与直线l2:y=x+1交于点P(2,m).
如图,过点(0,-2)的直线l1:y=kx+b(k≠0)与直线l2:y=x+1交于点P(2,m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com