
分析 根据平面向量的计算法则进行解答.
解答 解:原式=$\frac{1}{2}$×2$\overrightarrow{a}$+$\frac{1}{2}$×6$\overrightarrow{b}$-3$\overrightarrow{a}$,
=$\overrightarrow{a}$+3$\overrightarrow{b}$-3$\overrightarrow{a}$,
=-2$\overrightarrow{a}$+3$\overrightarrow{b}$,
故答案是:-2$\overrightarrow{a}$+3$\overrightarrow{b}$.
点评 本题考查了平面向量.解题时,利用了向量数乘的分配律和加法结合律.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
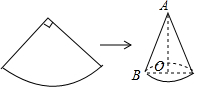 如图,现有一圆心角为90°,半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒(接缝忽略不计),用其它铁片再做一个圆形盖子把量筒底面密封.
如图,现有一圆心角为90°,半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒(接缝忽略不计),用其它铁片再做一个圆形盖子把量筒底面密封.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
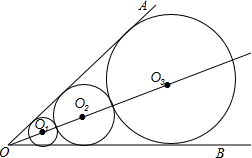 如图所示,已知∠AOB=60°,☉O1与∠AOB的两边都相切,沿OO1方向做☉O2与∠AOB的两边相切,且与☉O1外切,再作☉O3与∠AOB的两边相切,且与☉O2外切,…,如此作下去,☉On与∠AOB的两边相切,且与☉On-1外切,设☉On的半径为rn,已知r1=1则r2016=32015.
如图所示,已知∠AOB=60°,☉O1与∠AOB的两边都相切,沿OO1方向做☉O2与∠AOB的两边相切,且与☉O1外切,再作☉O3与∠AOB的两边相切,且与☉O2外切,…,如此作下去,☉On与∠AOB的两边相切,且与☉On-1外切,设☉On的半径为rn,已知r1=1则r2016=32015.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x-3)2-1 | B. | y=2(x+3)2-1 | C. | y=2x2+4 | D. | y=2x2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
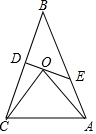 如图,在△ABC中,∠B=30°,点D是BC的中点,DE⊥BC交AB于点E,点O在DE上,OA=OC,OD=1,OE=2.5,则BE=7,AE=$\frac{9}{2}$.
如图,在△ABC中,∠B=30°,点D是BC的中点,DE⊥BC交AB于点E,点O在DE上,OA=OC,OD=1,OE=2.5,则BE=7,AE=$\frac{9}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com