
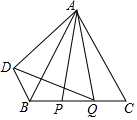
 如图,△ABC是等边三角形,AB=3cm,动点P、Q分别从点B,C同时出发,运动速度均为2cm/s,点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).
如图,△ABC是等边三角形,AB=3cm,动点P、Q分别从点B,C同时出发,运动速度均为2cm/s,点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).分析 (1)根据轴对称图形的性质证明BD=BP,然后求出PQ的长,由PQ=BD即可求出t的值.
(2)根据判定定理(SAS)证明即可.
(3)只需证明△ABP≌△ACQ、△ABD≌△ABP,再根据全等图形的性质即可证明△ADQ是等边三角形.
解答 (1)解:由题意可知:BP=2t,BQ=2t
∴PQ=3-4t
∵点P关于直线AB的对称点为D,
∴BP=BD
∴当PQ=BD时,有:3-4t=2t,t=$\frac{1}{2}$
即:当PQ=BD时,t=$\frac{1}{2}$
故答案为:$\frac{1}{2}$
(2)证明:∵△ABC是等边三角形,AB=3cm,
∴AB=AC=3cm,∠ABQ=∠ACP=60°
在△ACP与△ABQ中,$\left\{\begin{array}{l}{AB=AC(已证)}\\{∠ABQ=∠ACP=60°}\\{BQ=CP=2t+PQ}\end{array}\right.$
∴△ACP≌△ABQ(SAS)
(3)如图: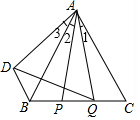
在△ABP与△ACQ中,$\left\{\begin{array}{l}{AB=AC=3cm}\\{∠ABP=∠ACQ=60°}\\{BP=CQ=2t}\end{array}\right.$
∴△ABP≌△ACQ(SAS)
又点P关于直线AB的对称点为D,
∴BD=BP,∠ABD=∠ABP
∴在△ABD与△ABP中,$\left\{\begin{array}{l}{BD=BP}\\{∠ABD=∠ABP}\\{AB=AB}\end{array}\right.$
∴△ABD≌△ABP(SAS)
∴△ACQ≌△ABD
∴∠1=∠3,AQ=AP=AD
∵∠1+∠BAQ=∠3+∠BAQ=60°
即:∠DAQ=60°
∴△ADQ是等边三角形.
点评 本题考查了几何图形的变换问题,解题的关键是掌握轴对称图形的性质、全等三角形的性质、等边三角形的性质及其综合应用.


科目:初中数学 来源: 题型:解答题
 如图,等边△ABC中,边长为5,D是BC上一点,∠EDF=60°.
如图,等边△ABC中,边长为5,D是BC上一点,∠EDF=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
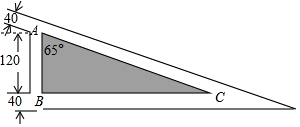 如图所示为某市生态绿化工程中的一幅大型绿化的平面图(单位:米)根据图示尺寸计算绿地(阴影部分-直角三角形)的面积(精确到0.1m)(参考数据sin65°=0.9063、cos65°=0.4226、tan65°=2.1445、cot65°=0.4663)
如图所示为某市生态绿化工程中的一幅大型绿化的平面图(单位:米)根据图示尺寸计算绿地(阴影部分-直角三角形)的面积(精确到0.1m)(参考数据sin65°=0.9063、cos65°=0.4226、tan65°=2.1445、cot65°=0.4663)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com