
如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为
30°,点B为直线l上的一个动点,延长AB至点C ,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.
,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.
(1)若点B的横坐标为6,则点C的坐标为(______,_____),DE的长为 ;
(2)若点B的横坐标大于3,则线段CF的长度是否发生改变?若不变,请求出线段CF的长度;若改变,请说明理由;
(3)连结BE,在点B的运动过程中,以OB为直径的⊙P与△ABE某一边所在的直线相切,请求出所
有满足条件的DE的长.

 (1点C的坐标为(______,_____),DE的长为 ;
(1点C的坐标为(______,_____),DE的长为 ;
(1)C(9, ) , DE=
) , DE= ; …………4分
; …………4分
(2)如图(1),过点A作AM⊥x轴于M ,
∴∠OAM=90°, ∠BOA=30°,
∴AM=OAtan∠BOA= .…………2分
.…………2分
∵B为AC的中点,
∴AB=BC
又∵AM∥CF,
∴∠AMB=∠CFB ,∠MAB=∠FCB,
∴⊿ABM≌⊿CBF
 ∴CF=AM=
∴CF=AM= .
.
∴线段CF的长度保持不变. …………2分
(3)如图1,过点B作BG⊥x轴于点G.
易证, OB=2BG ,CD=2BG,
∴OB=CD.
(I)当点D在点A的右侧时,⊙P只能与BE相切,如图2.
设DE=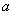 , 则OB=CD=
, 则OB=CD= .
.
∵ ⊙P与BE相切于点B,
⊙P与BE相切于点B,
∴OB⊥BE.
易得BF= EF=
EF= .
.
∴OF=OB+BF= .
.
∴OF=2DF,
 ∴
∴ =
= .
.
解得 .
.
∴ DE= . …………2分
. …………2分
(II)当点D在线段OA上时,
①若⊙P与直线AE相切,如图3,
 易得,直线l与AE的距离是
易得,直线l与AE的距离是 .
.
∴ OB=3.
∴ CD=3.
∴DE=2CF-CD=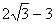 . …………2分
. …………2分
②当⊙P与AB相切,如 图4.
图4.
∴∠OBA=90°.
 ∴OB=OAtan∠OBA=
∴OB=OAtan∠OBA= .
.
∴CD= .
.
∴ DE=2CF-CD= =
= . …………1分
. …………1分
(III)当点D在点O的左侧时,⊙P只能与直线AE相切,如图5
∵ 直线l与AE的距离是 ,
,
∴ OB=3.
∴ CD=3.
∴ DE=2CF+CD= .
.
综上所述,DE的长为 或
或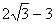 或
或 . …………1分
. …………1分


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
⊙A半径为5,圆心A的坐标为(1,0),点P的坐标为(-2,4),则点P与⊙A的位置关系是
A.点P在⊙A上 B.点P在⊙A 内 C.点P在⊙A外 D.点P在⊙A上或外
内 C.点P在⊙A外 D.点P在⊙A上或外
查看答案和解析>>
科目:初中数学 来源: 题型:
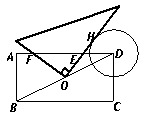
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则 的值为.( )
的值为.( )
A 1 B C  D 2
D 2
查看答案和解析>>
科目:初中数学 来源: 题型:
一只不透明的箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中随机摸出一个球是白球的概率是多少?
(2)从箱子中随机摸出一个球,记录下颜色后不将它放回箱子,搅匀后再摸出一个球,求两次摸出的球都是白球的概率,并画出树状图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com